0. Getting Started
A. Goals
The purpose of this assignment is to gain practice with object-oriented programming, bitwise operators, number systems, and cryptography. The specific goals are to:
- Continue to familiarize yourself with objects in Java.
- Understand the differences between static libraries and non-static objects.
- Implement practical examples of bits and bitwise functions.
- Get a glimpse into the world of modern cryptography. At the end of the assignment, you will be able to encrypt and decrypt text using a pseudo-random number stream, and reveal messages hidden into images.
B. Background
Encryption is the process of encoding messages or information that can only be decoded by people with authorization (usually some sort of key). Good encryption algorithms produce output that looks random to a bystander but is easily decipherable with the correct key.
In Hail, Caesar!, the key was a single character which shifted all characters in the message up the alphabet. This algorithm was far from perfect, and you demonstrated this by writing a function to crack the cipher without having authorization. This exploited the fact that the outputted cipher wasn’t entirely random – some letters appeared an abnormal amount, and this allowed you to find the offset key.
Over the two millennia since Julius Caesar, cryptography has gone a long way. Computers have played an enormous role in developing information communications as well as keeping those communications safe. In this assignment, you will implement and use a linear feedback shift register (LFSR) to create a stream of pseudo-random bits. This will help you create a significantly more random cipher in hw08.
Once you have written a crypto library, with the necessary functions, you will use it for a practical application in hw08: steganography — the practice of hiding secret messages in images in plain sight.
C. Understand the Problem
For this assignment, you will write an LFSR object. Once given a “seed”, it produces a boundless stream of seemingly random bits (1s and 0s). The key feature is that given the same seed, the LFSR will produce the same stream of bits. This means that if Alice and Bob both know the same seed, they can produce identical random bit streams.
To encrypt the message, you would perform an exclusive or (^) operation between each bit in the message and the LFSR’s sequence of pseudo-random bits. The resulting cipher, after you perform the XOR operations, will appear to be nonsense like Kao y{u(x kp }1rkz~|g2rjf@r), but when it is XORed again with the same sequence of pseudo-random bits as the first time, the encrypted message can be decrypted into the original message.
Since an LFSR’s bit stream is completely determined by its given parameters, Alice can produce the same bit stream that Bob used to encrypt a cipher if she knows the seed, and so can decrypt the message through the same process. For this reason, an LFSR encryption scheme is a symmetric key encryption technique (the alternative is an asymmetric scheme, in which different passwords are used for encrypting and decrypting). We will revisit the actual encryption on HW08.
D. Designing the Requirements and Interface
The readme will be in codio when you start the assignment, and you can download it here as well. You will be writing the following two classes from scratch. Their APIs are listed below, but each will be elaborated on in later sections of the homework. You must include all of the functions listed below in the class under which they are listed.
public class LFSR
-----------------
public LFSR(String seed, int tapPosition);
public LFSR(int seedLength, int tapPosition);
public String toString();
public int getTapPosition();
public int nextBit();
public class LFSRTest
------------------
In the LFSR class, you may add additional functions and/or instance variables you like, but they must be private. A public main for testing (prior to your JUnit testing) is fine, but no additional public functions or instance variables may be added.
1. Number Systems
A. Binary
Before we move onto writing code, it may be helpful to review number systems. You have been dealing with numbers your entire life - 10, 12, 100, 1, 50001. Something that is often missed in this numerical notation is the base of this number system, which is 10. For example 1210 = 1 * 103 + 2 * 102 + 1 * 101 + 0 * 100. Likewise 5030110 = 5 * 106 + 0 * 105 + 3 * 104 + 0 * 103 + 1 * 102 + 1 * 101 + 0 * 100. This is inherent to us, we have ten toes and ten fingers. However, computers only understand 1s and 0s (it has to do with electric signals). Hence, we must be able to communicate all data to a computer in binary numbers comprised of just 1s and 0s as digits. We call these binary digits bits for short.
The binary number system represents numbers in base 2 and deals with powers of 2. For example, 310 = 1 * 21 + 1 * 20 = 112. Likewise 5010 = 1 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = 1100102. In this way we can translate numbers from the binary system to decimal and vice-versa. This paragraph is the extent of what you need to know about binary to complete this assignment, but you might find conversions between binary and decimal enlightening.

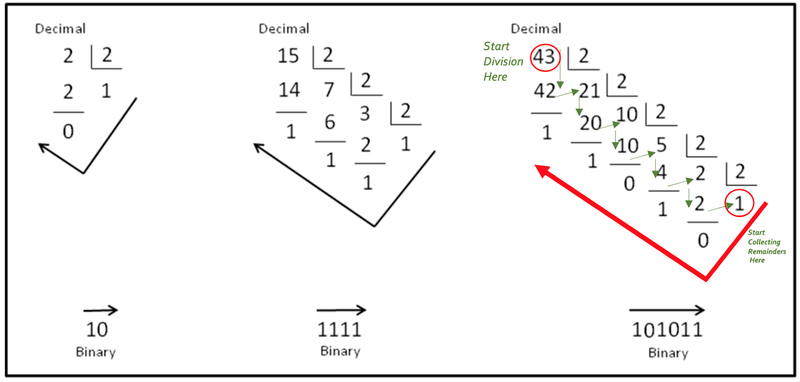
The diagram above illustrates an easy way to convert from decimal to binary. Here we use long division as a manner of conversion. In the diagram shown below, take a look at the two examples on the right. Either of these examples can be divided into four diagonals (follow the diagonal from upper left to bottom right) of numbers.
Consider the rightmost example below. The uppermost diagonal is the divisor which will always be 2. The second diagonal (43, 21, 10…..) is the diagonal of dividends/quotients and the bottom most diagonal (1, 1, 0…..) is the diagonal of remainders. The way we proceed is - we divide 43 by 2 which gives 21 as the quotient and 1 as the remainder. 21 then becomes the new dividend and we divide it by 2 to get 10 as the quotient and 1 as the remainder. Progressing in this manner, we end up with 1 as the dividend which we divide by 2 to get 0 as the quotient and 1 as the remainder. We now take the remainders in the opposite direction (from the last remainder back up to the first) to get our binary number which is 1010112 (for the decimal number 4310).
B. Exclusive Or (XOR)
Exclusive Or, or XOR, is a binary operation like the operations and + or. It is expressed in Java with the ^ operator. It behaves on like so:
x |
y |
x ^ y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Note that ^ as an operator works on int values like 0 and 1, but also on the boolean values true and false, too, where 1 represents true and 0 represents false. It even works for char values '1' and '0'! For example:
int trueResult = 1 ^ 0; // evaluates to 1
boolean falseResult = true ^ true; // evaluates to false
char charResult = '0' ^ '1'; // evaluates to 1 (not '1')
2. LFSR
A. Understanding the Problem
In the first part of this assignment, you will be creating a linear feedback shift register (LFSR). An LFSR is a structure that can produce a stream of pseudo-random bits, which has many practical uses, particularly in cryptography.
The LFSR consists of a register of bits and a tap position. The register is simply a list of bits that has a fixed size (which should suggest to you a good data structure to implement the LFSR). The tap position is simply an index in the register of bits that will be used to create the pseudo-random bits later. When we create an LFSR, we must seed it by providing the initial values in the register.
There are two steps in producing a pseudo-random bit with a given LFSR:
- Shift all bits by one place towards the most significant bit/MSB (the leftmost bit in the diagram).
- Then, replace the least significant bit/LSB (the rightmost bit) with the exclusive or of the most significant bit that was shifted off of the register and the bit previously in the tap position.
The new least significant bit (rightmost in the diagram) will be the pseudo-random bit produced by the LFSR.
Consider the example below. The following figure shows an LFSR seeded with the initial seed 01101000010 and tap position 8 during the process of producing one pseudo-random bit. Keep in mind that the tap position is counted from the rightmost (least significant) bit! This is opposite from the way positions are counted in arrays and strings, but is consistent with the way bit/digit positions are counted in numbers. The first step mentioned above, shifting all the bits one place towards the MSB is designated by the grey arrows separating the two arrays. The second step mentioned above, XORing two bits and replacing the LSB with that result, is shown via the blue-highlighted boxes.
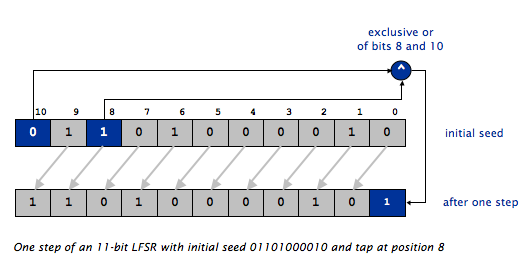
NOTE THAT THE ARRAY INDICES ARE FROM 10 (left) to 0 (right). This is opposite from how most arrays are diagrammed.
B. Shift Register Implementation
Before you begin writing your LFSR.java class, you will want to decide how you want to represent the register of bits within your class. We are leaving this decision up to you, and any working implementation will be accepted. Here are our suggestions:
- an
int[]containing only 1s and 0s - a
char[]containing only ‘1’s and ‘0’s - a
boolean[]containing only true and false - a single
int, where each bit represents a position in the shift register. This is a more challenging implementation, but will give you a chance to play around with and understand bits and binary better. In this case, your shift register will be limited to 32 bits, and you will need to use the bitwise operators&(bitwise AND),|(bitwise OR),<<(shift left), and>>(shift right).
C. Constructor and Methods
Your LFSR class will implement the API described below. This section will provide the details for the constructor and methods:
public class LFSR
-----------------
public LFSR(String seed, int tapPosition) // constructor
public LFSR(int seedLength, int tapPosition) // constructor for a random seed
public String toString() // string representation of the LFSR
public int getTapPosition() // return the tap position
public int nextBit() // return a random bit and update the LFSR
public LFSR(String seed, int tapPosition) takes a String parameter seed whose characters are a sequence of 0s and 1s, and an int parameter tapPosition specifying which position in the register to use as the tap. The constructor should throw an IllegalArgumentException with a useful error message if seed is null, if seed contains any characters other than 0 or 1, or if tapPosition refers to an impossible position in the register (for example, -1).
Here is an example of how to throw an IllegalArgumentException with a useful error message in your code:
public void printCharAt(String s, int index) {
if (index < 0 || index >= s.length()) {
// the String argument to the IAException is the error message
throw new IllegalArgumentException("Can't print a character at an invalid index.");
} else {
System.out.println(s.charAt(index));
}
}
Note: remember the String.charAt() method, which will be helpful when parsing through seed.
public LFSR(int seedLength, int tapPosition) takes an int parameter seedLength, and generates a random seed (i.e. a random string of 0s and 1s of length seedLength.
The constructor should throw an IllegalArgumentException with a useful error message if seedLength is not positive or if tapPosition refers to an impossible position in the register.
public String toString() returns the current bit sequence in the shift register as a String of 1s and 0s. For example, the code below should print 101011. This method will help you when debugging.
LFSR lfsr = new LFSR("101011", 3);
System.out.println(lfsr.toString());
Note: Make sure your toString() method works! If it doesn’t, all of our automated tests will fail and you will lose lots and lots of points.
public int getTapPosition() returns the tap position, as given by the constructor.
public int nextBit() performs one step of the LFSR, as described in section 2A and returns the least significant bit (the rightmost bit) in the shift register after the step has been performed as an int with the value 0 or 1.
For testing, you should ensure you can run
LFSR lfsr = new LFSR("01101000010", 8);
for (int i = 0; i < 10; i++) {
int bit = lfsr.nextBit();
System.out.println(lfsr.toString() + " " + bit);
}
which should print
11010000101 1
10100001011 1
01000010110 0
10000101100 0
00001011001 1
00010110010 0
00101100100 0
01011001001 1
10110010010 0
01100100100 0
3. JUnit Testing
Now, implement a series of JUnit tests for your LFSR.java class in LFSRTest.java, which is given to you, or you can download it here. Verifying the correctness of your LFSR will be crucial for hw08, which will rely heavily upon your implementation here.
You should provide tests for the public methods in LFSR.java, as well as the constructors. To refresh your memory, those methods are:
public class LFSR
-----------------
public LFSR(String seed, int tapPosition) // constructor
public LFSR(int seedLength, int tapPosition) // constructor for a random seed
public String toString() // string representation of the LFSR
public int getTapPosition() // return the tap position
public int nextBit() // return a random bit and update the LFSR
Specifically, each method should have at least one test for each of the possible situations:
- An exception is purposely thrown by the method (if the method throws an exception)
- A case which emphasizes typical functionality of the method
- An edge case, if possible, for the function
Keep in mind for the second constructor that because the generated seed will be random, you will not be able to test for what seed specifically is stored in your register. However, you can still test that the register is initialized properly. You also should still be able to test that IllegalArgumentExceptions are thrown properly.
Here is how to write a test that passes when the unit of code throws an IllegalArgumentException using the expected syntax:
@Test(expected = IllegalArgumentException.class)
public void testConstructorWithNullSeed() {
// should throw exception when seed is null
LFSR broken = new LFSR(null, 5);
}
Another thing to keep in mind is that you cannot access your register directly due to encapsulation. However, you can use your toString() method to retrieve a string representation of it that you can use in your tests instead. This is an aspect of good design because it allows you, the programmer, to later change how you implemented your register (if you wanted to) without needing to change any of your tests. Since toString() and getTapPosition() will be tested implicitly, you do not need to make individual tests for these methods.
4. README and Submission
A. README
Complete readme_steg_pt1.txt in the same way you have done for previous assignments.
B. Submission
Submit LFSR.java, LFSRTest.java, and readme_steg_pt1.txt on Gradescope.
Gradescope will output the following style error: Using a static member import should be avoided - org.junit.Assert.*. This can be ignored.
Before submission, comment out any print statements that were used for debugging or testing your functions and not any print statements that we asked you to insert.
Be sure that every method has an appropriate header comment, and that your code is well-documented.