TAG formalism

The primitive elements of the standard TAG formalism are known as elementary trees. ELEMENTARY TREES are of two types: initial trees and auxiliary trees (see Figure 2.1). In describing natural language, INITIAL TREES are minimal linguistic structures that contain no recursion, i.e. trees containing the phrasal structure of simple sentences, NP's, PP's, and so forth. Initial trees are characterized by the following: 1) all internal nodes are labeled by non-terminals, 2) all leaf nodes are labeled by terminals, or by non-terminal nodes marked for substitution. An initial tree is called an X-type initial tree if its root is labeled with type X.

{Elementary trees in TAG

 

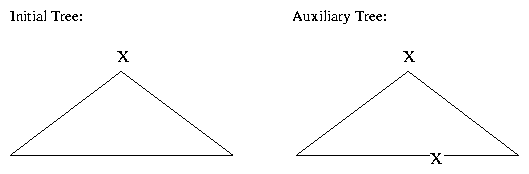
Recursive structures are represented by AUXILIARY TREES, which represent constituents that are adjuncts to basic structures (e.g. adverbials). Auxiliary trees are characterized as follows: 1) all internal nodes are labeled by non-terminals, 2) all leaf nodes are labeled by terminals, or by non-terminal nodes marked for substitution, except for exactly one non-terminal node, called the foot node, which can only be used to adjoin the tree to another node^2.1, 3) the foot node has the same label as the root node of the tree. There are two operations defined in the TAG formalism, substitution^2.2 and adjunction. In the SUBSTITUTION operation, the root node on an initial tree is merged into a non-terminal leaf node marked for substitution in another initial tree, producing a new tree. The root node and the substitution node must have the same name. Figure 2.2 shows two initial trees and the tree resulting from the substitution of one tree into the other.

{Substitution in TAG

 

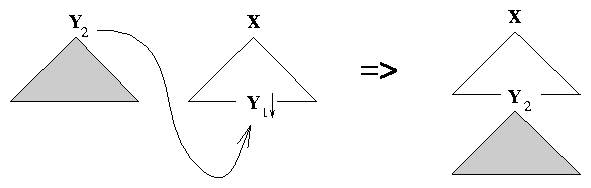
In an ADJUNCTION operation, an auxiliary tree is grafted onto a non-terminal node anywhere in an initial tree. The root and foot nodes of the auxiliary tree must match the node at which the auxiliary tree adjoins. Figure 2.3 shows an auxiliary tree and an initial tree, and the tree resulting from an adjunction operation.

{Adjunction in TAG

 

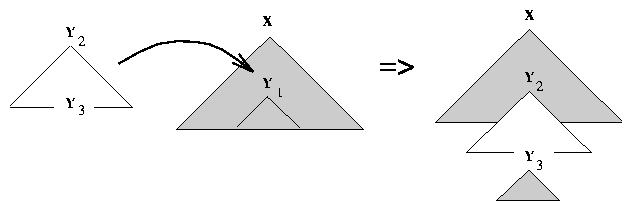
A TAG G is a collection of finite initial trees, I, and auxiliary trees, A. The TREE SET of a TAG G, ${\cal T}(G)$ is defined to be the set of all derived trees starting from S-type initial trees in I whose frontier consists of terminal nodes (all substitution nodes having been filled). The STRING LANGUAGE generated by a TAG, ${\cal L}(G)$, is defined to be the set of all terminal strings on the frontier of the trees in ${\cal T}(G)$.