


Next: Pseudo-coordination
Up: Conjunction
Previous: To as a Conjunction
This section describes the method for predicative coordination
(including VP coordination of various kinds) used in XTAG. The
description is derived from work described in ([#!anoopjoshi96!#]).
It is important to say that this implementation of predicative
coordination is not part of the XTAG release at the moment due massive
parsing ambiguities. This is partly because of the current
implementation and also the inherent ambiguities due to VP
coordination that cause a combinatorial explosion for the parser. We
are trying to remedy both of these limitations using a probability
model for coordination attachments which will be included as part of a
later XTAG release.
This extended domain of locality in a lexicalized Tree Adjoining
Grammar causes problems when we consider the coordination of such
predicates. Consider ((385)) for instance, the NP the beans that I bought from Alice in the Right-Node Raising (RNR) construction
has to be shared by the two elementary trees (which are anchored by
cooked and ate respectively).
(384)0(384
- (385)
- (((Harry cooked) and (Mary ate)) the beans that I bought from Alice)
We use the standard notion of coordination which is shown in
Figure 21.10 which maps two constituents of like type,
but with different interpretations, into a constituent of the same
type.
Figure 21.10:
Coordination schema
|
|
We add a new operation to the LTAG formalism (in addition to
substitution and adjunction) called conjoin (later we discuss an
alternative which replaces this operation by the traditional
operations of substitution and adjunction). While substitution and
adjunction take two trees to give a derived tree, conjoin
takes three trees and composes them to give a derived tree. One of
the trees is always the tree obtained by specializing the schema in
Figure 21.10 for a particular category. The tree obtained
will be a lexicalized tree, with the lexical anchor as the
conjunction: and, but, etc.
The conjoin operation then creates a contraction between nodes
in the contraction sets of the trees being coordinated. The term contraction is taken from the graph-theoretic notion of edge
contraction. In a graph, when an edge joining two vertices is
contracted, the nodes are merged and the new vertex retains edges to
the union of the neighbors of the merged vertices. The conjoin
operation supplies a new edge between each corresponding node in the
contraction set and then contracts that edge.
For example, applying conjoin to the trees Conj(and),
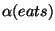 and
and
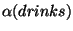 gives us the derivation tree and
derived structure for the constituent in (386) shown in
Figure 21.11.
gives us the derivation tree and
derived structure for the constituent in (386) shown in
Figure 21.11.
(385)0(385
- (386)
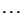 eats cookies and drinks beer
eats cookies and drinks beer
Figure:
An example of the conjoin operation. 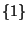 denotes a shared dependency.
denotes a shared dependency.
|
|
Another way of viewing the conjoin operation is as the construction of
an auxiliary structure from an elementary tree. For example, from the
elementary tree
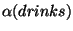 ,
the conjoin operation would create
the auxiliary structure
,
the conjoin operation would create
the auxiliary structure
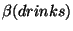 shown in
Figure 21.12. The adjunction operation would now be
responsible for creating contractions between nodes in the contraction
sets of the two trees supplied to it. Such an approach is attractive
for two reasons. First, it uses only the traditional operations of
substitution and adjunction. Secondly, it treats conj X as a
kind of ``modifier'' on the left conjunct X. This approach
reduces some of the parsing ambiguities introduced by the predicative
coordination trees and forms the basis of the XTAG implementation.
shown in
Figure 21.12. The adjunction operation would now be
responsible for creating contractions between nodes in the contraction
sets of the two trees supplied to it. Such an approach is attractive
for two reasons. First, it uses only the traditional operations of
substitution and adjunction. Secondly, it treats conj X as a
kind of ``modifier'' on the left conjunct X. This approach
reduces some of the parsing ambiguities introduced by the predicative
coordination trees and forms the basis of the XTAG implementation.
Figure 21.12:
Coordination as adjunction.
|
|
More information about predicative coordination can be found in
([#!anoopjoshi96!#]), including an extension to handle gapping constructions.



Next: Pseudo-coordination
Up: Conjunction
Previous: To as a Conjunction
XTAG Project
1998-09-14
![\includegraphics[scale=1.1]{/mnt/linc/xtag/work/doc/tech-rept/ps/conj-files/conj.ps}](img232.gif)