| Topological Sort |
Programming Assignment |
Update 29 November 2012 Since the TopologicalSort constructor to read in a graph file is so challenging, and needs to work for the actual sorting, we are providing a library that you may use on homework 9 only to read in the graph. You may not use this for homework 8.
If you want to use our graph reading library, download GraphReader.class and save it to the folder with your TopologicalSort.java. Then you can replace your constructor with the following:
public class TopologicalSort {
private Vertex[] vertices;
public TopologicalSort(String fname) {
vertices = GraphReader.read(fname);
}
}
Revised Submission Policy For hw08, you only need to complete TopologicalSort(String filename) and getVertices(). The complete assignment will be due Tuesday, 4 December at 9:00pm. You will submit the completed program as hw09. To avoid accidentally submitting the first part as hw09, hw09 will not open for submission until after the late period for hw08 ends.
- For hw08 (due this Thursday), you may leave code related to topological sort in your program, but your code must compile, and it must not modify the graph structure you create when you read in the file in any way. We will ignore this code, and will not grade it for correctness or style. You must include the getVertices() method as well as the constructor, or you will receive a significant point deduction because we will not be able to test your prgoram.
- For hw09 (due next Tuesday), you must submit a complete program as described in the assignment below. It must include the constructor that reads in a graph file, but we will not grade it.
- If you have completed the entire assignment, you may request that we grade your topological sort as well in the modified readme file. In that case you will receive one additional extra credit point, but you will not be allowed to submit a revised version for hw09. If you answer no or submit the original readme file, we will only grade your constructor and getVertices(). You will be allowed to submit .graph files for extra credit on hw09 even if you submit the complete program as hw09.
Updated tips for this assignment. Based on the experience in office hours so far, we are making the following additional suggestions that will be incorporated into future versions of the assignment:
- Review the LinkedStackOfDoubles.java from lecture to understand how to work with linked lists in Java. In particular, look at the size() method as an example of how to find your way from the beginning of a linked list to the end.
- Review the FloodFill.java example from lecture to understand how depth-first search works. This example does not used linked lists, but the algorithm is the same. The key is to think of every pixel in the image as a vertex that is connected to the pixels above, below, left, and right of it.
- We have provided code to test your constructor on piazza: https://piazza.com/class#fall2012/cis110/784. Cut and paste this code into your class. Then you can right a two-line main function that creates a TopologicalSort object and calls its printGraph() method.
- Work on your program in very small steps. After each step, make sure your program compiles, and if possible test it. For example, when you write your constructor, write only the code to read in the vertices. Compile your program. Add the code from piazza and write a main function to create a graph and print it. It should print the number of vertices and list their names. Don't move on to reading edges from the .graph file until this works.
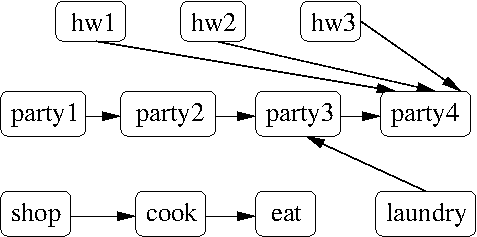
Background. Imagine you are planning out your schedule for the week. Aside from fixed tasks, like attending class and recitation, you have many tasks you can schedule at will. Perhaps you have three assignments due at the end of the week in three different classes, you want to party four times, you need to do laundry, cook dinner, eat, and go shopping. Some of these tasks are independent--it doesn't really matter what order you do your three assignments in, for example. But other tasks do depend on one another. You have to go shopping before you cook, and you have to cook before you eat. Perhaps you need to do laundry before your third party, and you have decided not to party the fourth time until all your assignments are done. The question is, what order should you do your tasks in?
Graphs. Any time you have a problem involving relationships between things, you should think "graph problem." A graph consists of a series of vertices that represent your things, and edges connecting them that represent your relationships. Since we are interested in one-way relationships like "after," we will use directed edges that have an arrow pointing from one vertex to the other. So the graph that models your tasks for the week would look like this, where an edge point from task A to task B means "task B must happen after task A":
Representing a graph. There are many different ways to represent a graph in Java. We will use a simple data structure that works well when there are relatively few edges in the graph. We will store the vertices in an array vertices[], and refer to them by their index in the array. So vertex i means the vertex stored at vertices[i].
Vertex class. Each vertex stores a linked list edges of the edges leaving it. It also stores a string name for referring to it. The purpose of name is strictly descriptive -- for example, when you are planning out your week, this would be store the task name. If we were making a full-fledged, object-oriented design, we would make the name and edges instance variables private and provide methods to manipulate. But each of those methods would have only one or two lines of code, and we would be complicated the program rather than simplifying it. Instead, we just make the name and edges variables public.
public class Vertex {
public String name; // the task associated with this vertex
public VertexList edges; // linked list of edges to other vertices
}
VertexList class. The list of edges is equally simple, but subtler. Each node in the linked list v.edges represents and edge leaving v. The only additional piece of information we need for the edge is which vertex it leads to. Of course, we also need a pointer to the next node in the linked list. Another way of thinking about this is that v.edges is just a list of vertices that can be reached directly from v. Once again, this class is so simple that we make the instance variables public rather than saddling it with lots of single-line methods.
public class VertexList {
public VertexList next; // next node in linked list of vertices
public int target; // index of target vertex of this edge
}
Topological Sort. Now let us return to the original problem. Your goal is to order your tasks so that you only start one task after any tasks it depends on are completed. In terms of the graph structure, this means you want to order the vertices so that each vertex is listed after any vertices that lead to it. On other words, if the vertex v1 is listed before the vertex v2, there must not be any sequence of edges that leads from v2 back to v1. This problem is called topological sorting, and is a classic application of depth-first search.
The idea is to start by finding the vertices that have no incoming edges. In the example, these correspond to tasks that do not depend on anything else, i.e. that you could start immediately. Specifically:
- Create an empty linked list order of type VertexList that will keep track of the topological order of vertices.
- Find the vertices that have no incoming edges. These vertices can safely appear anywhere in the ordered list because they do not depend on any other vertices. For each vertex with no incoming edges, carry out the following steps:
- Mark the vertex as visited.
- For each of its outgoing edges, check the vertex the edges leads to. If that vertex is not marked as visited, recursively carry out steps 3-5.
- After all outgoing edges have been visited, add this vertex to the front of order.
Your Program. Write a class TopologicalSort with the following API. We recommend implementing and testing the methods in the order they are described in the paragraphs below.
public class TopologicalSort
-----------------------------------------------------------------------------------------
TopologicalSort(String filename) // read in a graph from filename
Vertex[] getVertices() // return the array of vertices in the graph
VertexList getSortedVertices() // return a linked list of vertices
// in topologically sorted order
String vertexNames(String join) // return the vertex names in the
// original order, with the string
// join inserted between each pair
String orderedNames(String join) // return the vertex names in sorted
// order, with the string join
// inserted between each pair
Additional methods and instance variables. You will need some instance variables, e.g. to store your graph. You will also need additional helper methods, at the very least for topological sorting. You may create whatever methods and instance variables you need, but all of them must be private because they are internal details of your class. Only the methods listed above (and the main function) should be public, and these must all conform exactly to the API. Your program should rely only on Vertex and VertexList. You may not modify these, nor may your write any helper classes of your own. Everything should be in the TopologicalSort class.
Data files. Download data.zip and unzip it into the same folder where you write your program. This includes the Vertex and VertexList classes, and some simple test cases. If you are working on the lab computers, you will likely need to download In.java and Out.java here. Place them in the same folder as your TopologicalSort.java.
TopologicalSort(String filename). Your constructor should read in an input file (use the In class from the book's standard library) whose first line contains the number N of vertices. Each of the following N lines is a string, which you should store as the names of the N vertices. Following this will be a series of lines containing two numbers like this:
v1 v2
These are edges: the first number is the index of the starting vertex, and the second number is the index of the target vertex. For each edge listed, create a VertexList object with the target v2, and add it to the back of the edges list in vertex v1. This is not the simplest order to implement, but it is the most intuitive and will make later steps easier to debug.
Make sure to follow this rule precisely so that your program will output the same topological ordering as our reference implementation. We will be directly comparing your output to ours, and will deduct points if your ordering differs, even if you also produce a valid ordering (there is often more than one possibility)
The list of edges ends either at the end of the file, or when it reads a line
-1 -1
Everything after that line should be ignored. That way it is possible to include a description of the graph as a long comment at the end of the file. The input file for the example at the top of the assignment looks like this:
11 hw1 hw2 hw3 party1 party2 party3 party4 laundry cook eat shop 3 4 4 5 5 6 8 9 10 8 7 5 0 6 1 6 2 6 -1 -1
Reading and writing files using In and Out. The book's standard library includes classes for reading and writing file called In and Out. They are very similar to StdIn and StdOut, but work for any file. You will find more information about them in Section 3.1 of the book and booksite, and in the corresponding lecture slides.
Idiosyncrasies of In. The name of each vertex is stored in as a line of text in the input file, and it may contain spaces. You should use the readLine() method of In rather than readString() to handle this. There is an annoying idiosyncrasy though: when you read the number of vertices using readInt(), the newline character at the end fo the first line remains in the file. As a result, your first call to readLine() will return a blank line. To get around this, you should call readLine() once as soon as your read the number of vertices, and before you start reading in the vertex names.
Error Checking, break, and continue. You may assume that the input file is correctly formatted, except that some edges may point to non-existent vertices. You should ignore any such edges.
When you are testing for invalid edges, or for "-1 -1", you will find the break and continue statements useful. break ends for and while loops immediately, without executing the rest of the body or the update statement of the for loop, and without checking the continuation condition. continue immediately goes to the next loop iteration. It skips over the rest of the body, but does execute the update statement in for loops, and checks the continuation condition. If you create boolean variables called isValidEdge and isEndEdge that are true when the edge is valid and when the edge is "-1 -1", you can include the following statements inside the loop that reads edges to handle these cases:
if ( isEndEdge) break; if (!isValidEdge) continue;
Testing TopologicalSort(). Write a main function that reads in a graph, then prints out a new graph file. You should be able to save the output file using output redirection (the > operator on the command line), or you can write it directly to a file using the Out class. The graph you produce should be valid (you should be able to use it as input to your program), and it should include exactly the same vertices and edges as the original file. Keep in mind that your output file will not necessarily list the edges in the same order as the input file. That is fine. You can decide which command line arguments your main function will expect. You should also plan on expanding main to test other methods as you implement them. Leave your main in the program when you submit.
String vertexNames(String join). Return the names of the vertices in their original order, separated by the string join. For example, if the vertex names are A, B, C, D, and E, vertexNames(":") would return "A:B:C:D:E". Update main to test this method.
getVertices(). getVertices() should return the array of vertices. This will probably be a one-line method. Update main to test it. We need this method to test and grade your program. (If we didn't need this for grading, we would recommend against including it. getVertices() effectively gives client programs access to the internal details of your graph. This violates good design principles because it allows other programs to muck with your data.)
String orderedNames(String join). Works like vertexNames(), but prints the vertices in topologically sorted order. You have the option of calling your topological sort methods from orderedNames(), or you may call them from the constructor and save the result in an instance variable. Either way, now is the time to implement topological sorting. Update main to test this method.
getSortedVertices(). getSortedVertices() should return the linked list of vertices in topologically sorted order. This will probably be one or two lines, depending on where you call your topological sort methods. Like getVertices(), this method is included for grading.
Debugging. Linked data structures can be extremely tricky to debug. Start by testing with simple examples that have only a few vertices and edges, then gradually increase the complexity. Any time you modify your code, start over with the simplest tests to make sure nothing has broken. For each test, draw out the graph on paper, and write out the order in which the edges leaving each vertex will be stored. Compare the graph your main prints out to the paper version and make sure they match.
Next, write out on paper the exact order that your algorithm will visit the graph edges, when it will mark vertices, and when it will add vertices to the order. Add print statements to your topological sort code where each of these steps occurs so you can compare the results.
Collaboration. As always, you may not share code. However you are encouraged to work together in designing test graphs and in working out the order in which everything will be visited on paper. Don't forget to list anyone you work with in your readme file.
Extra Credit. Design one or more interesting graphs of your own. The graphs must have a different structure than the provided examples. Your graph must not contain any cycles (any sequence of edges that loops back to where you started), because topological sort is not defined on such graphs. Make sure to end the edge list with "-1 -1", and follow that with a comment. The comment should include your name, "University of Pennsylvania, CIS 110 Fall 2012", and a description of graph if appropriate. We will include especially creative examples in future versions of the assignment.
Checklist. There is no checklist for this assignment. Instead, we have tried to incorporate the usual checklist information, such as possible progress steps and testing, into the assignment itself.
Submission. Submit TopologicalSort.java, and a completed readme_topologicalsort.txt. If you do the extra credit, submit a zip file extra_graphs.zip containing your graphs.
This assignment was developed by Benedict BrownCopyright © 2012