Goals

• Strengthen C++ and use the C++ Standard Library
• Afterwards you should (hopefully) comfortable enough with C++ containers to complete leet-code or interview style questions in C++ :)
• More familiarity with Finite State Machines
• Understanding and appreciation for NFAs and Regeular Expressions as useful tools!

Collaboration

For assignments in CIS 3990, you will complete each of them on your own. However, you may discuss high-level ideas with other students, but any viewing, sharing, copying, or dictating of code is forbidden. If you are worried about whether something violates academic integrity, please post on Ed or contact the instructor(s).

Setup

You can downlowd the starter files into your environment by running the following command. You should run it from inside your git repository since that is how you will submit your code.

curl -o nfa_starter.zip https://www.seas.upenn.edu/~tqmcgaha/cis3990/current/projects/code/nfa_starter.zip

You can also download the files manually here if you would like: nfa_starter.zip

From here, you need to extract the files by running

unzip nfa_starter.zip

You should now have a folder called nfa that has the starter files. We expect this to be a folder inside the base of your github repository, similar to cowsay and check-setup. If you accidentally put the folder somewhere else, you can move it with the mv command in the terminal.

Starter Files

In the zip you will find several files:

The first two are important directly for the work you will do:

• NFA.hpp: Contains the declarations and extensive comments detailing the object and the memeber functions you will have to implement for this assignment.
• Makefile: Makefile for compilng the tests and source code. This is here because you will likely want to targets and source files to the project.

The rest are related to the tests suite:

• ParseNFA.hpp: Contains the declarations for a function to parse a NFA from a string.
• ParseNFA.cpp: Contains the implementation for the ParseNFA function.
• test_nfa.cpp: The tests that we will be using to evaluate your NFA implementation.
• test_suite.cpp: Entry point for running our tests.
• catch.cpp: Catch2 testing framework source
• catch.hpp: Catch2 testing framework source

We recommend reading all of NFA.hpp before you get started on the assignment.

Overview

The goal of this assignment is to have you tackle a more “algorithmically” challenging problem in C++ and getting you familiar with the C++ standard library containers. We will do this by implementing a mini grep program and an NFA class that supports matching regular expressions for our grep program.

What is an NFA

An NFA is a variant on a the finite state machines we handled in the previous assignment. If you need a refresher on what a FSM is, you should reread that section of the hw2 spec.

Notably, there are two primary categories for finite state machines. Deterministic finite automatons (DFAs) and Non-deterministic finite automatons (NFAs). What we did in the previous assignment was implement a DFA. We made the following assumptions:

• Each transition has a unique combination of source state and input to cause the transition
• The only way to move between states is by processing another symbol of input.

In an NFA, we do not need to follow these assumptions. However, all DFAs are NFAs (in some sense you can think of all possible DFAs as a subset of all possible NFAs).

Duplicate Transitions

First we will explain how duplicate transitions work. Consider the following NFA:

This NFA is used to determine if there is a 1 three positions from the end of a binary string. (assume we are start and end anchored). Lets walk through this example with the sample input string “1000”.

We start at the node marked with the “start” arrow and begin parsing the string one character at a time to transition us between states.

Our first input is the character 1. Normally we would transfer to one state, but note here we have two possible transitions to take. Which one do we end up taking? Both. We consider both possibile transitions that could be taken. If it helps, you can reason aoub this by thinking that we are in two (or more) states “at the same time”.

Then the machine handles the next character 0, which “moves” us in two ways. We move from the start state to stay in the start state (cause there is an edge on the 0 input that cycles back to that state) AND we move from the state labeled “third” to the state labeled “second”:

We then get another 0 which does somehitng similar.

If we aren’t end anchored then we would consider this a success as we have reached the end state, but in this example we are assuming we are end anchored. Next is 0, which again keeps us in the starting state, but we are also no longer in the “end” state since there is no transition from the end state that has input “0”.

Epsilon Transitions

Next we will talk about the second assumption that DFA’s make, and how they do not apply to NFAs. In NFAs we have a special transition called an “epsilon transition” marked by the epsilon character \(\varepsilon\) These transitions are sort of “free moves” where the machine doesn’t have to parse any input to make the transition.

Since it is a “Free move” then we run into a similar situation as the previous section. Does the machine take the epsilon transition or does it stay in its current state? Like the previous rule, we look at both cases.

Here is an example NFA that matches to any string that starts with NFA or DFA and has any number of trailing A’s.

Lets run through it with the input “DFAAA” When the machine starts, it starts in two states. There is the indicated start state, and an epsilon transition from that state to another.

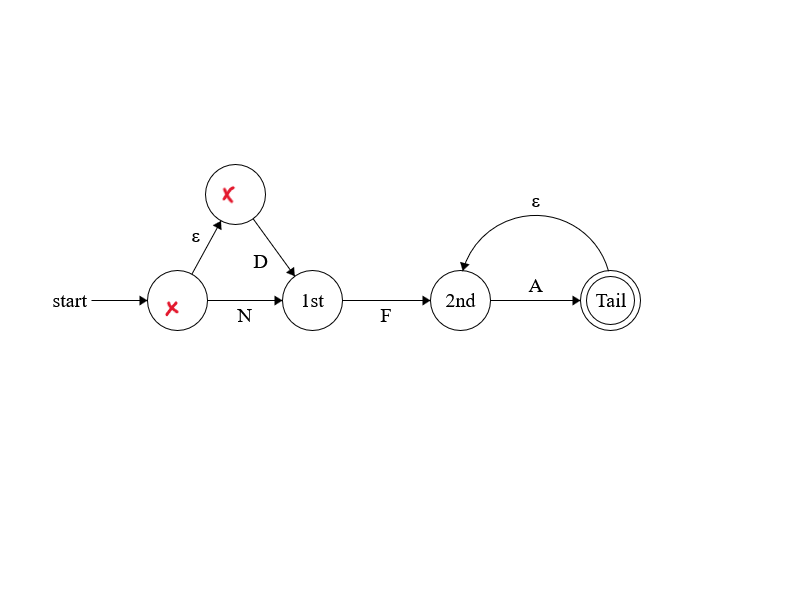
Then we process the first character “D” which moves from the top state onwards. The machine “drops” its memory of having been in the start state since there is no “D” transition from there to another state.

Like a normal FSM, the next character “F” moves the machine to the next state

Then we reach the first “A” which moves the machine forward, but the resulting state has an epsilon transition back to the state we are in, so the machine exists in both states:

The second “A” effectively repeats the above move. Since the state marked “tail” doesn’t have an A transition so is “dropped”. The state marked “2nd” does have an “A” transition so it moves onto the tail state (which has an epsilon back to the “2nd” state

In this case, we would state that we have “matched” the input to the NFA.

Other Details

Other than the conceptual details there are a few other detail worth noting:

• We don’t have to make our own data structures, we have the C++ standard library
• Since the machine can be in multiple states, it can match to multiple states, so your NFA::Match should return an unordered_set of all the StateIDs it matched to.
• We use a special character value k_epsilon_transition defined in NFA.hpp to represent epsilon transitions.

Tips

Suggested Headers

The C++ standard library is hugeeeeeeeeee, so instead of making you crawl through all of it, there are a few headers that you may find useful. You are not required to use all or any of these if you don’t want to. There also may be headers outside of these that you find useful, but these ones are probably the ones you want to use.

• unordered_map
• unordered_set
• map
• set
• vector
• string
• pair
• algorithm

Custom Types in associative containers

If you want to store a custom type in an associative container map/unordered_map/set/unordered_set then you need to make sure some extra things are defined to support that type. If you use something like StateID (which is just an unsigned integer) then you don’t need to do these.

map and set

For map and set, then the key in the map or value in the set must support the < operator since these data structures are ordered.

For example, if I had a custom struct Thing I would need to define either of these and the data structures map and set will use it automatically.

// as a member function
bool Thing::operator<(const Thing& other) {
  // return true iff `this` is less than other
}

// as a non-member function
bool opeartor<(const Thing& lhs, const Thing& rhs) {
  // return true iff lhs is less than rhs.
}

unordered

The unordered equivalents unordered_map and unordered_set are implemented as hash map and hash set. So if the value in the set or the key in the map is a custom type, we must define how to hash our types. If we are using a custom type Thing then we must define:

template<>
struct std::hash<Thing> {
  std::size_t operator()(const Thing& t) const {
    // TODO: calculate the hash code of t here and return it
  }
};

You must also define operator== on Thing:

// as a member function
bool Thing::operator==(const Thing& other) {
  // return true iff `this` is equal to other
}

// as a non-member function
bool opeartor==(const Thing& lhs, const Thing& rhs) {
  // return true iff lhs is equal to rhs.
}

Approaches to implementing an NFA

While this looks very similar to an FSM, you likely will not be able to copy much of your FSM code. Part of this is due to the problem being different, and part of this is just that you have better data structure available to you to make the code better.

One particular quirk to the NFA is handling being in multiple states at once. There are two possible ways of doing this.

1. One way is to implement an epsilon closure algorithm so that you can create an equivalent FSM from the NFA and just call match() on that. This algorithm is not something we go over in this class, but if you know it already or want to look into it yourself, you can.
2. The suggested (and probably simpler implementation) is to just to “be in multiple states at once” which is how we described an NFA. One hiccup to this tho is that it can be complicated and you need to be aware of any epsilon cycles that may show up in your NFA. Consider the NFA below that matches to a string that starts with B, ends with T and has any number of A’s inbetween them. If you aren’t careful, then your code could end up in an infinitely loop as it tries to navigate all epsilon states it could be in. (Due to the epsilon cycle between 2nd and 3rd). Cycles can be more complicated than this, this is just one example.

Banned Headers

As of right now there is only one banned header: <regex> which is sort of what we are implementing in this assignment :)

Grading & Testing

Compilation

We have supplied you with a Makefile that can be used for compiling your code into an executable. To do this, open the terminal and then type in make.

You may need to resolve any compiler warnings and compiler errors that show up. Once all compiler errors have been resolved, if you ls in the terminal, you should be able to see an executable called test_suite. You can then run this by typing in ./test_suite to see the evaluation of your code.

Note that your submission will be partially evaluated on the number of compiler warnings. You should eliminate ALL compiler warnings in your code.

Valgrind

We will also test your submission on whether there are any memory errors or memory leaks. We will be using valgrind to do this. To do this, you should try running: valgrind --leak-check=full ./test_suite

If everything is correct, you should see the following towards the bottom of the output:

 ==1620== All heap blocks were freed -- no leaks are possible
 ==1620==
 ==1620== For counts of detected and suppressed errors, rerun with: -v
 ==1620== ERROR SUMMARY: 0 errors from 0 contexts (suppressed: 0 from 0)

If you do not see something similar to the above in your output, valgrind will have printed out details about where the errors and memory leaks occurred.

catch2

As with mentioned above, you can compile the your implementation by using the make command. This will result in several output files, including an executable called test_suite.

After compiling your solution with make, You can run all of the tests for the homwork by invoking:

$ ./test_suite

You can also run only specific tests by passing command line arguments into test_suite

For example, to only run the “Binary Even Length” test, you can type in:

$ ./test_suite "Binary Even Length"

You can specify which tests are run for any of the tests in the assingment. You just need to know the names of the tests, and you can do this by running:

$ ./test_suite --list-tests

These settings can be helpful for debugging specific parts of the assignment, especially since test_suite can be run with these settings through valgrind and gdb!

Code Quality

For this assignment, we will be checking the quality of your code in two ways:

• Through automated checks with clang-format & clang-tidy
• Through manually reviewing your code for any style issues.

Clang Format and Clang Tidy

The makefile we provided with this assignment is configured to help make sure your code is properly formatted and follows good (modern) C++ coding conventions.

To do this, we make use of two tools: clang-format and clang-tidy

To make sure your code identation is nice, we have clang-format. All you need to do to use this utility, is to run make format, which will run the tool and indent your code propely. Code that is turned in is expected to follow the specified style, code that is ill-formated must be fixed and re-submitted.

clang-tidy is a more complicated tool. Part of it is checking for style and readability issues but that is not all it does. It also checks for and can detect possible bugs in your program.

Because of all this, we are enforcing that your code does not produce any clang-tidy errors. You can run clang-tidy on your code by running: make tidy-check. Note that you will have to fix any compiler errors before clang-tidy will run (and be useful).

If you have any questions about understanding an error, please ask on Ed discussion and we will happily assist you.

Submission

Please submit your completed code to Gradescope via your github repo. We will be checking for compilation warnings, valgrind errors, making sure the test_suite runs correctly, and that you did not violate any rules established in the specification.