Homework 3: Hail, Caesar! and Sierpinski

A. Goals

The goals of the first half of this assignment are to practice using functions, arrays, and strings in java, as well as learn about the field of cryptography. The specific goals include:

to write and use functions, and understand the use of helper functions,
use and manipulate arrays,
learn about String manipulation and ASCII encoding, and
learn about cryptography and its history.

At the end of the assignment, you will have a program that can encrypt and decrypt the Caesar cipher.

Bust of Julius Caesar — Julius Caesar, Roman Statesman

B. Background

Cryptography is the study of secure communications and secret codes. It helps you, say, send a secret message across enemy lines, knowing that even if the message is intercepted, it could not be read. People have been using ciphers (encrypted messages) for thousands of years, but only in the last century have computers come into the field. One of the oldest ways to hide a message is to use a substitution cipher. One classic example of a substitution cipher is the Caesar cipher, named after the first recorded (and most famous) user, Julius Caesar. If you'd like to learn more about the Caesar cipher, you can check out the wikipedia page to read about its history and usage.

C. Understanding the Problem

The Caesar cipher is a basic encryption technique where all letters in a message are shifted down the alphabet by a certain number. In order to encrypt or decrypt a message, you will need a secret key that should, in practice, be hard to find if you don’t already know it. In the Caesar cipher, the key is the number of places to shift each character. This number could be specified numerically (e.g., 4) or it could be specified as a character (e.g., 'E' -- which is 4 places over from 'A'). To make it simpler, we typically convert the entire message to uppercase, and may omit punctuation.

For instance, consider the message (and famous Julius Caesar quote): "CAESAR’S WIFE MUST BE ABOVE SUSPICION" and the key "E", which says to shift each letter to the right four places in the alphabet. For example, 'C' becomes 'G', 'A' becomes 'E', etc. Note the letter 'W' in "WIFE", when shifted four down, goes beyond 'Z'. This is handled by wrapping back to the front of the alphabet, and so 'W' becomes 'A'.

In total, the message becomes:

GEIWEV'W AMJI QYWX FI EFSZI WYWTMGMSR

D. Program Requirements and Interface

By the end of this assignment, you will have a Caesar program takes in command line arguments that will tell it whether to

encrypt a message using a particular key, or
decrypt a message using a particular key

The message will be stored in a file, which will be read by the program.

To encrypt the message stored in plaintext.txt with a key of 'G', you would call

 java Caesar encrypt plaintext.txt G

To decrypt the message stored in cipher.txt with a key of 'G', you would call

 java Caesar decrypt cipher.txt G

E. Getting Started

Begin by creating a main class file named Caesar.java. Be sure to put all of your code in this file. Also download the following files and store them in the same directory: english.txt, encrypted_message.txt, and readme_caesar.txt.

A. Understanding the Representation

Before we begin encrypting messages, we first need to decide how to represent a message in our program. The obvious choice would be to store them as a String. This would certainly work, but may not be the easiest approach.

Instead, we will represent the message as an array of integers, where each integer is a symbol in the message. All English letters will be represented by their place in the alphabet. For instance, "C" is the third letter in the alphabet, and so would be represented by a 2. Remember, computer science loves zero-indexing, so the first letter, "A", would be 0. The word "CONSUL" would be represented as [ 2, 14, 13, 18, 20, 11 ].

Recall that Java already encodes characters as integers using ASCII:

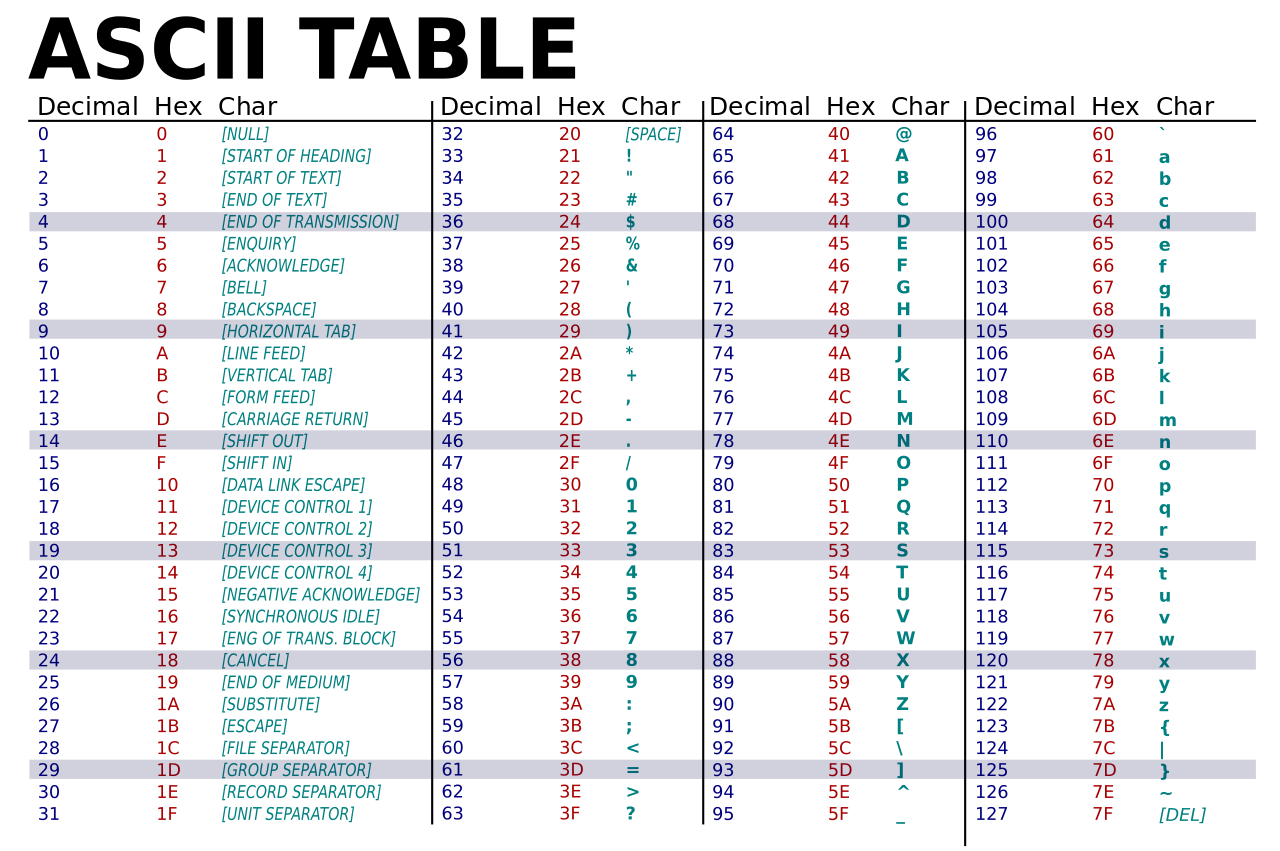
There is no need to memorize this, since we can easily recover the integer encoding via casting. For instance, take a look at this code snippet:

char letter = ‘A’;

// cast letter to an integer as encoded by ASCII
int asciiRepresentation = (int) letter;

// will print out 65
System.out.println(asciiRepresentation);

We could certainly use ASCII to encode characters as integers in this program, but the math is a bit easier if we instead represent 'A' as 0 instead of 65. Fortunately, there is a very simple way of converting between the ASCII encoding and our symbol encoding. We can simply subtract or add the character 'A':

char letter = ‘C’;

// cast letter to an integer as encoded by our representation
int ourSymbolRepresentation = (int) letter - 'A';

// will print out 2
System.out.println(ourSymbolRepresentation);

We can easily recover the original character simply by adding 'A' to it:

int ourSymbolRepresentation = 2;

// will become 'C'
char letter = (char) (ourSymbolRepresentation + 'A');

You should play around in the interactions pane so to fully understand how to make this switch, before moving on to the next section.

B. Program Structure Decomposition

Recall that functions allow us to intelligently decompose our program into a collection of logical units that we can develop and test independently. We can often identify these major units by considering the high level structure of our program and what we will need to do.

Recall that your Caesar program must take in command line arguments that will tell it whether to

encrypt a message using a particular key, or
decrypt a message using a particular key,

The message will be stored in a file, which will be read by the program.

Based solely on this description, we can see that we will need two high-level functions:

encrypt(), and
decrypt(),

The main() will then serve as the overall control for our program, reading the command line arguments, reading in the text from the file, and calling the appropriate functions.

We can also see that many of these functions will need to convert between text and the integer symbol encoding, and handle the shifting. In fact, these procedures are likely to be so common that we should make helper functions to handle them.

For example, our basic encryption/decryption process will need to:

take in text as a String and convert it into our symbol encoding
shift that encoding either right (to encrypt) or left (to decrypt)
convert that symbol encoding back into text for output

With this decomposition, our task will then be to write functions for each of these major units (which we can do and test independently), and then combine those functions together into a working program.

C. Converting To and From Symbol Arrays

We will first tackle the lowest-level functions to handle encoding/decoding of strings (items 1 and 3 in the last list above) by writing two functions: one to convert from a String to our symbol representation (an array of integers), and one to convert from our symbol representation (an array of integers) to a String:

/*
 * Description: converts a string to a symbol array,
 *              where each element of the array is an
 *              integer encoding of the corresponding
 *              element of the string.
 * Input:  the message text to be converted
 * Output: integer encoding of the message
 */
public static int[] stringToSymbolArray(String str) { ... }

/*
 * Description: converts an array of symbols to a string,
 *              where each element of the array is an
 *              integer encoding of the corresponding
 *              element of the string.
 * Input:  integer encoding of the message
 * Output: the message text
 */
public static String symbolArrayToString(int[] symbols) { ... }

stringToSymbolArray() should initialize an integer array of the correct length, iterate through each character in str to fill in the indices in the array with the corresponding symbol integer value. Recall that you can use str.charAt(i) to find the ith character in str and your knowledge of ASCII to make the conversion from char to the symbol integer.

Note: you should use the str.toUpperCase() before converting. This will simply make all alphabet characters become uppercase.

Test this first function by writing a bit of test code in your main() function to call stringToSymbolArray("CONSUL") and check that the function call returns the array [ 2, 14, 13, 18, 20, 11 ]. Try a few other test cases. Once you're convinced the function is working, move on to write symbolArrayToString().

symbolArrayToString() should take an integer array where each element is the symbol value for the corresponding letter. The structure of this function is similar to stringToSymbolArray(), except it reverses the process.

Again, write code in main() to test symbolArrayToString(). Since you know that stringToSymbolArray() is working, your test code can use this function to encode a simple string, and then use symbolArrayToString() to decode it. If it works correctly, you should get back the same simple string you encoded. Test your code until you're convinced both functions work.

D. Shifting Symbols

The next step is to write a function to handle the shifting. We can define it as:

 public static int shift(int symbol, int offset)

If symbol is an english letter (between 0 and 25), then it should be shifted down the alphabet by offset amount (an integer between 0 and 25). Remember to wrap symbols that go off the alphabet (‘W’ shifted by ‘E’ should return 0 representing ‘A’)!

If symbol is not between 0 and 25, meaning it is some sort of whitespace or punctuation, then it should just be returned as is. (In our implementation, punctuation is not encoded and does not change during the encryption/decryption process.)

Hint: Modulo (%) will be helpful here!

Write an appropriate header comment for your shift() function.

E. Unshifting Symbols

It may also be helpful for us to handle the unshifting (i.e., left shifting) of characters. Write a function to unshift the characters:

 public static int unshift(int symbol, int offset)

This should simply undo the shifts done by shift(). Try thinking about how you will do this and do some examples before writing any code! Also, try to think how you can very easily do this by building on code you've already written.

F. Other Functions

While writing your program, you may find it useful to define other helper functions for processes that you are doing repeatedly. Feel free to define whatever other functions you need to while writing your program.

Now that we've defined functions to handle the encoding/decoding and shifting, we can focus on the two high-level functions in our program decomposition:

encrypt(), and
decrypt(),

The main() will then serve as the overall control for our program, reading the command line arguments, reading the text from the file, and calling the appropriate functions.

We will start by defining encrypt()....

A. Encrypt

Using the functions you have already written, you should write the function:

 public static String encrypt(String message, int key)

The basic operations carried out in the function should be to:

convert the message to an array of symbols (which we represent as ints)
for each alphabetic symbol in the array, shift it by the given key
return a String version of the encrypted symbol array

Once this is done, you should be able to test encrypt() in main() and be able to encrypt "ET TU, BRUTE?" using 6 (letter G) as the key to get "KZ ZA, HXAZK?".

Be sure to write good header comments for the function, and test it thoroughly before proceeding to the next part.

B. Decrypt

Now that you can encrypt your message, you need to be sure you can decrypt it. Write the decrypt function:

 public static String decrypt(String cipher, int key)

The structure of this function is very similar to encrypt(), but instead of using shift, you should be using unshift.

Once this is done, you should be able to use decrypt() in main() with "KZ ZA, HXAZK?" and 6 (letter G) as the key to obtain "ET TU, BRUTE?".

You should add some code in main() to test it. At this point, if you run a string through encrypt() and then decrypt(), the output should be the same as the input string.

Try putting this or something similar in your main():

String message = "I AM CONSTANT AS THE NORTHERN STAR";
String cipher = encrypt(message, /* some key */);
String decrypted = decrypt(cipher, /* same key */);
System.out.println(decrypted); // should be the original message (in upper case)

C. Reading From a File

Once you are confident that encrypt() and decrypt() are working, you should comment out anything you’ve written in your main(). In order to obtain the message you will be encrypting you will need to read in data from a file.

Look back at your NBody.java from last week and make use of In inStream to do this. The function that will be most helpful is inStream.readAll() which returns the entire text of the file as a String.

Write code in main to handle the command line arguments, load the specified text file, call the appropriate function to encrypt/decrypt the message, and output the result.

Before you move on to the next part, you should be able to run

 java Caesar encrypt filename.txt G

(filename.txt is not a file we provide)

to encrypt the message in filename.txt using G (symbol value 6) as the key, and

 java Caesar decrypt filename.txt G

to decrypt the message in filename.txt using G (symbol value 6) as the key.

(filename.txt is not a file we provide)

If you’d like a refresher on command-line arguments or reading from a file, you can look at NBody.

A. Goals

The purpose of the Recursive Graphics portion of this assignment is to gain practice with recursion.

Learn about iterated fractal systems
Use recursion

B. Background

Read sections 2.1–2.3 of Sedgewick & Wayne. Review the H-Tree example from the textbook and lecture.

The Sierpinski triangle is an example of a fractal pattern, like the H-tree pattern from Section 2.3 of the textbook. The Polish mathematician Wacław Sierpiński described the pattern in 1915, but it has appeared in Italian art since the 13th century. Though the Sierpinski triangle looks complex, it can be generated with a short recursive program. Your tasks are to write a recursive program that draws the Sierpinski triangle and a second program that draws another design of your choosing using recursion.

This is a Sierpinski triangle:

Here's a fractal in polymer clay and a Sierpinski valentine. Have a fractal cookie, a Sierpinski hamentashen, or a Sierpinski candy corn video (check out her other videos while you're at it!):

Write a program Sierpinski.java that recursively draws a Sierpinski triangle using PennDraw.

A. The `triangle()` function

First, write a function triangle() that takes a side length sideLength and a pair of coordinates (x, y) as parameters and uses PennDraw.filledPolygon() to draw a filled, downard-pointing equilateral triangle. You may use whichever form of PennDraw.filledPolygon() you prefer. It is up to you whether to define your triangle() function such that x and y specify the location of the triangle center, a particular vertex, or any other position in the triangle.

You can make your triangles any color(s) you like, but the background must be white. (We will be printing your figures to grade, and colored backgrounds use a tremendous amount of ink.)

Use the figure below to work out the coordinates of the other two vertices of the triangle, given one vertex:

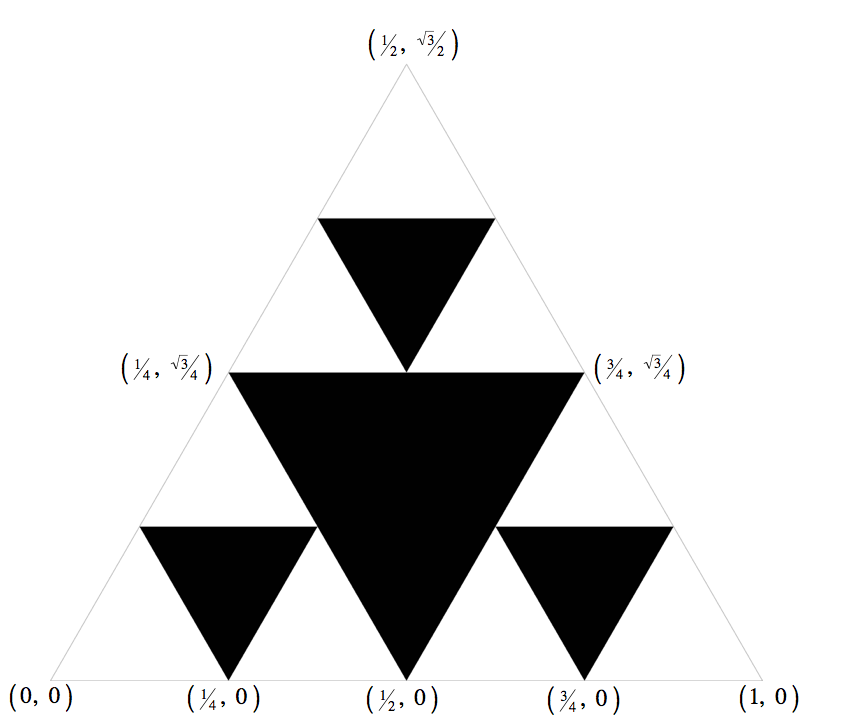
Make sure that your code compiles.

B. The `main()` function

Write a main() function that calls your triangle() function to draw a triangle with sides of length 0.5 with the bottom vertex located at (0.5, 0).

Later you will modify main() to draw the full Sierpinski triangle.

When you compile and run your program, you should see a triangle in the bottom center of your window.

C. Setting up the recursive structure of `sierpinski()`

Write a function sierpinski() that takes two parameters, numLevels and size. Your function should print numLevels and size, before recursively calling itself three times with the arguments numLevels - 1 and size / 2. The recursion should stop when numLevels is less than 1. Later, you will replace the print statements with a call to triangle().

Modify main() to interpret its first command-line argument as numLevels. Have it call sierpinski(numLevels, 0.5). You may assume that your program will be run with exactly one command-line argument that is a positive integer.

Make sure that your code compiles.

D. Checkpoint

Running your program with the following command-line arguments should produce the following output:

          > java Sierpinski 0

(no output)

> java Sierpinski 1
          1 0.5

> java Sierpinski 2
          2 0.5
          1 0.25
          1 0.25
          1 0.25

> java Sierpinski 3
          3 0.5
          2 0.25
          1 0.125
          1 0.125
          1 0.125
          2 0.25
          1 0.125
          1 0.125
          1 0.125
          2 0.25
          1 0.125
          1 0.125
          1 0.125

E. Drawing the Sierpinski triangle in `sierpinski()`

Comment out the print statements from Sierpinski().

Modify sierpinski() to take two additional arguments, x and y, and draw a Sierpinski triangle of order numLevels of size size with the triangle's reference point you use in the triangle() function.

Think recursively. A Sierpinski triangle of order numLevels comprises just a solid triangle and three smaller Sierpinski triangles, each half the size of the original, each of order numLevels - 1, to the left and right and above it. You have already written the function to draw the triangle and the recursion code from the previous steps – now, you only need to make the correct function calls.

Warning Do not call, PennDraw.setCanvasSize(), or PennDraw.save(). These functions will break our test scripts, and you will receive a large point deduction.

F. Checkpoint

Running your program with the command-line arguments below should produce the following output. (The figures below have a light outline around the triangle for illustration. You do not need to draw this outline in your own program.)


`> java Sierpinski 1`	`> java Sierpinski 2`	`> java Sierpinski 3`

`> java Sierpinski 4`	`> java Sierpinski 5`	`> java Sierpinski 6`

G. Animating

Once you have your Sierpinski triangle working, add calls to PennDraw.enableAnimation() and PennDraw.advance() into your sierpinski() function. (You are not required to animate your Sierpinski triangle, and it is not worth any points, but it is fun and will help you visualize the recursion. If you do add animation, leave it in your code: it will not affect our grading scripts.)

Experiment with different arrangements of the recursive calls to sierpinski() and your call to the triangle() function.

A. README

Complete readme_caesar.txt in the same way you have done for previous assignments.

B. Submission

Submit Caesar.java, Sierpinski.java and readme_caesar.txt on the course website. If you have any relevant extra files please mention this in the readme, and submit it compressed as extra.zip.

Before submission remove any print statements that were used for debugging or testing your functions.

Be sure that every method has an appropriate header comment, and that your code is well-documented.

Homework 3: Hail, Caesar! and Sierpinski

A. Goals

B. Background

C. Understanding the Problem

D. Program Requirements and Interface

E. Getting Started

A. Understanding the Representation

B. Program Structure Decomposition

C. Converting To and From Symbol Arrays

D. Shifting Symbols

E. Unshifting Symbols

F. Other Functions

A. Encrypt

B. Decrypt

C. Reading From a File

A. Goals

B. Background

A. The triangle() function

B. The main() function

C. Setting up the recursive structure of sierpinski()

D. Checkpoint

E. Drawing the Sierpinski triangle in sierpinski()

F. Checkpoint

G. Animating

A. README

B. Submission

A. The `triangle()` function

B. The `main()` function

C. Setting up the recursive structure of `sierpinski()`

E. Drawing the Sierpinski triangle in `sierpinski()`