Homework 6: Recursive Graphics

A. Goals

The purpose of the Recursive Graphics assignment is to gain practice with recursion.

• Learn about iterated fractal systems
• Use recursion

B. Background

Read sections 2.1–2.3 of Sedgewick & Wayne. Review the H-Tree example from the textbook and lecture.

The Sierpinski triangle is an example of a fractal pattern, like the H-tree pattern from Section 2.3 of the textbook. The Polish mathematician Wacław Sierpiński described the pattern in 1915, but it has appeared in Italian art since the 13th century. Though the Sierpinski triangle looks complex, it can be generated with a short recursive program. Your tasks are to write a recursive program that draws the Sierpinski triangle and a second program that draws another design of your choosing using recursion.

This is a Sierpinski triangle:

Here's a fractal in polymer clay and a Sierpinski valentine. Have a fractal cookie, a Sierpinski hamentashen, or a Sierpinski candy corn video (check out her other videos while you're at it!):

Write a program Sierpinski.java that recursively draws a Sierpinski triangle using StdDraw.

A. The triangle() function

First, write a function triangle() that takes a length and a pair of coordinates (x, y) as parameters and uses StdDraw.filledPolygon() to draw a filled equilateral triangle (with a vertex at the bottom). It is up to you whether to define your triangle() function such that x and y specify the location of the triangle center, a particular vertex, or any other position in the triangle.

You can make your triangle any color you like.

Use the figure below to work out the coordinates of the other two vertices of the triangle, given one vertex:

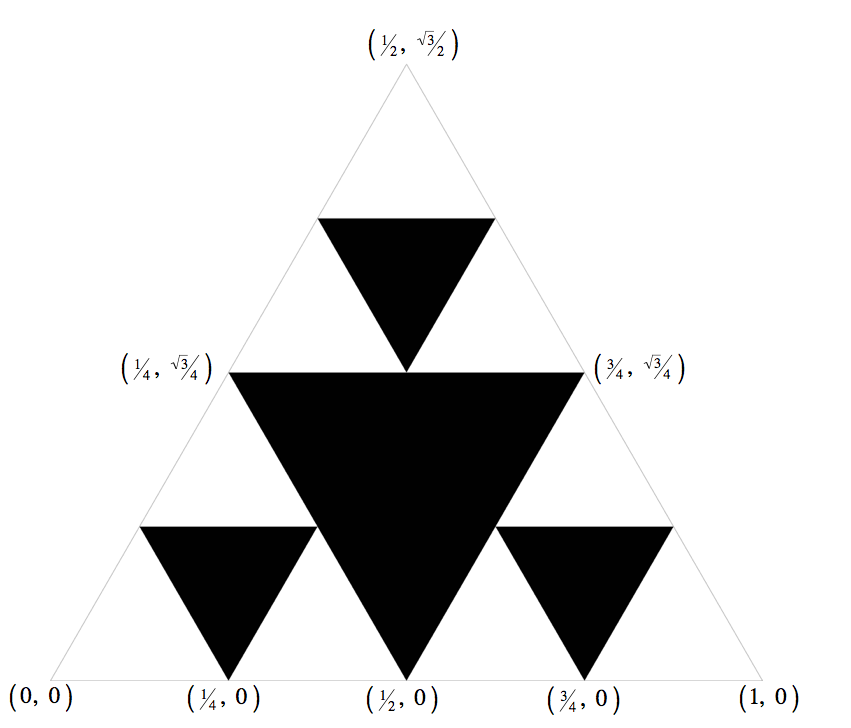
Make sure that your code compiles.

B. The main() function

Write a main() function that calls your triangle() function to draw a triangle with sides of length 0.5 with the bottom vertex located at (0.5, 0).

Later you will modify main() to draw the full Sierpinski triangle.

When you compile and run your program, you should see a triangle in the bottom center of your window.

C. Setting up the recursive structure of sierpinski()

Write a function sierpinski() that takes two parameters, n and size. Your function should print n and size, before recursively calling itself three times with the arguments n - 1 and size / 2. The recursion should stop when n is 0. Later, you will replace the print statements with a call to triangle().

Modify main() to take one integer, command-line argument N and have it call sierpinski(N, 0.5). You may assume that your program will be run with exactly one command-line argument that is a positive integer.

Make sure that your code compiles.

D. Checkpoint

Running your program with the following command-line arguments should produce the following output:

> java Sierpinski 0

(no output)

> java Sierpinski 1
1 0.5

> java Sierpinski 2
2 0.5
1 0.25
1 0.25
1 0.25

> java Sierpinski 3
3 0.5
2 0.25
1 0.125
1 0.125
1 0.125
2 0.25
1 0.125
1 0.125
1 0.125
2 0.25
1 0.125
1 0.125
1 0.125

E. Drawing the Sierpinski triangle in sierpinski

Remove the print statements from Sierpinski().

Modify sierpinski() to take two additional arguments, x and y, and draw a Sierpinski triangle of order n of size size with a vertex at (x, y).

Think recursively. A Sierpinski triangle of order n comprises just a solid triangle and three smaller Sierpinski triangles, each half the size of the original, each of order n - 1, to the left and right and above it. You have already written the function to draw the triangle and the recursion code from the previous steps – now, you only need to make the correct function calls.

Warning Do not call StdDraw.setXscale(), StdDraw.setYscale(), StdDraw.setCanvasSize(), or StdDraw.save(). These functions will break our test scripts, and you will receive a large point deduction.

F. Checkpoint

Running your program with the below command-line arguments should produce the following output. (The figures below have a light outline around the triangle for illustration. You do not need to draw this outline in your own program.)

> java Sierpinski 1	> java Sierpinski 2	> java Sierpinski 3
> java Sierpinski 4	> java Sierpinski 5	> java Sierpinski 6

G. Animating

Once you have your Sierpinski triangle working, add a call to StdDraw.show(10) into your sierpinski() function.

Experiment with different arrangements of the recursive calls to sierpinski() and your call to the triangle() function.

In this part you will create your own recursive pattern. Write a program Art.java that takes one integer command-line argument N to control the depth of the recursion and produces a recursive pattern of your own choosing.

It's up to you what to write, as long as it follows the rules below.

• The pattern can be based on recursively drawing a pattern, like Sierpinski, on recursive subdivision, like the dragon curve or fractal Brownian motion, or on any combination of the two. But it must be recursive (sorry, no Mandelbrot fractals – they're very cool, but they aren't recursive).
• The recursive structures of your program must be different from Sierpinski, H-Tree, and Brownian – just changing the triangle in Sierpinski to a square, for example, is not enough. If the number of recursive calls is different, or the order in which the calls are made is different, you should be fine.
• Your program must take one command-line argument. If your recursive function takes multiple parameters, you can choose some of the values that have the best effect, and do something like the following:

  if      (N == 1) { x = 0.55; y = 0.75; n = 3; }
  else if (N == 2) { x = 0.55; y = 0.75; n = 5; }
  else if (N == 3) { x = 0.32; y = 0.71; n = 8; }
  else if ...
  

• Your program must not be tail-recursive. Tail recursive functions make only a single recursive call at the very beginning or end of the function.
• Your drawing must stay within the unit square (the area between 0 and 1 in both x- and y-coordinates).
• Your Art.java cannot have interactive features that depend upon keyboard or mouse input: you may not call StdDraw.hasNextKeyTyped(), StdDraw.nextKeyTyped(), StdDraw.mouseX(), StdDraw.mouseY(), or StdDraw.mousePressed().
• The same warning as for Sierpinski.java applies: do not call StdDraw.setXscale(), StdDraw.setYscale(), StdDraw.setCanvasSize(), or StdDraw.save(). These functions will break our test scripts, and you will receive a large point deduction.
• You may optionally submit a .zip file containing any additional images, sound or other data required for your program. Your program can rely on animation for effect if you wish, as long as it is recursive.

Extra credit You will receive up to two points of extra credit for especially creative submissions, as judged by your TA. Extra credit will be rewarded not only for especially cool recursion, but also for especially cool designs, even if the recursion is fairly simple. As long as your Art.java meets the minimum requirements (takes one command-line argument, is not tail-recursive, stays within the unit square, and is fundamentally different from our examples), it will be eligible for extra credit.

Be creative and have fun!

Warning Teaching staff are unable to answer questions such as "Is my Art.java good enough to get full credit?" or "Is my Art.java cool enough to get extra credit?" You will need to decide for yourself. We do not grade homework before it is submitted, and we will not promise in advance that something is correct.

Examples

Check out the Famous Fractals in Fractals Unleashed, and Wikipedia's list of fractals by Hausdorff dimension. Some pictures are harder to generate than others (and some require trig); consult a TA for advice if you're unsure.

Some examples from the lists above that fulfill the requirements for Art.java are shown below.

Cantor Set	Sierpinski Carpet
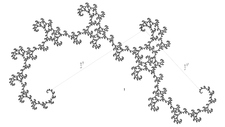
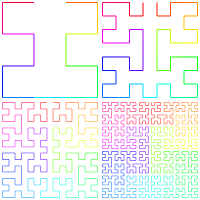
Dragon Curve	Moore Curve

Submit a completed readme_recursivegraphics.txt, Sierpinski.java, Art.java, and if desired, an extra.zip file containing any supplementary files needed by Art.java.