In grouping, our research are motivated by two set of questions,1) how to extract “interesting” patterns from data, I believe grouping is a general computational engine in perception, and 2) how to guide the grouping process to achieve specific vision tasks, such as recognizing familiar object shapes.
Guilding the segmentation process to detect familiar objects
Concurrent Object Segmentation and Recognition with Graph Partitioning
Stella Yu and Ralph
Gross and Jianbo Shi
Neural Information Processing Systems, NIPS, December 2002
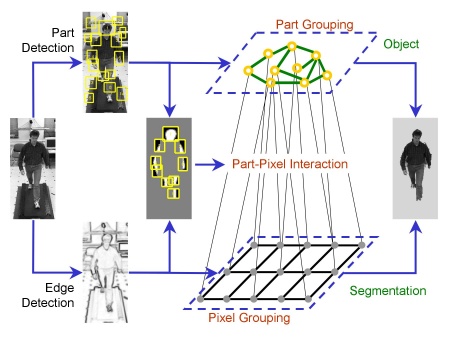
This is our work towards achieve body detection and segmentation in one step.
As a side result, we are able to label the body parts as we computes its
segmentation from the background.
Learning Segmentation with Random Walk
Marina Maila and Jianbo
Shi
Neural Information Processing Systems(NIPS,) 2001.
We interpret the pair-wise pixel similarity as edge flows in a Markov random
walk, and study the eigenvalues and the eigenvectors of the transition matrix.
We show that the Ncut graph partition function measures the probability of
a particle jumping between two groups. With this interpretation of Ncut,
we developed an algorithm that can learn to set up the “right” graph weights
using training examples.
Stella X. YU and Jianbo SHI
Technical report CMU-RI-TR-01-21, Robotics Institute, Carnegie Mellon University,
2001.
For several years, we have been trying to include object shape cue with region
segmentation. One main problem is that the shape and region similarity each
defines a different graph topology in the image space: the edges live in
between the pixels. Our solution is somewhat similar to the line progress
idea used in the German&German’s MRF paper. We construct two similarity
graphs, one using object shape cue, and one using region color/texture cue.
We show that the edge similarity graph can be transformed to the pixel similarity
graph using pixel-to-edge incident relationship matrix. This allows us to
combine the two energy functions into one, and use Ncut to segment the image
according to both cues. We have shown results on the synthetic images. Currently
we are working on extracting reliable shape similarity in real images. This
turns out to be very hard.
Extracting Interesting Patterns
"Normalized Cuts and Image Segmentation"
IEEE Transactions on Pattern Analysis and Machine Intelligence(PAMI) 2000. paper .
A prelimiary version appeared in
IEEE Conf. Computer Vision and Pattern Recognition(CVPR), June 1997, Puerto Rico
This is our original paper on this topic. After playing around different image segmentation algorithms, We come to realize that image segmentation is really a problem of “how to see the big picture in a scene?” There are almost infinite ways an image can be sub-divided, they are all technically correct, but most of them are not what we see, and do not “look pleasing”. We want the segmentation boundary look like what an artist would draw, from the big picture to detail. The second realization we made is that, grouping and segmentation is really the same process. By grouping pixels together, we are separating them away from each other, and by segmenting image regions, we are actually grouping each set of pixels. Therefore, the grouping process should pay a cost of segmentation, and vice visa.
Together, these goals lead to the Normalized Cuts graph partition cost function, which measures the segmentation cost, and it is exactly the dual of the Normalized Association graph partition cost function, which measures the grouping cost. This problem is NP-hard, and we are also very concerned with computation process of avoiding local minima. This leads to finding a global optimal solution in the continuous space using eigen-decomposition.
"Understanding Popout through Repulsion"
Stella Yu and Jianbo Shi
IEEE Conf. On Computer Vision and Pattern Recognition (CVPR), Kauai, Hawaii, December 11-13, 2001. paper
In this paper, we ask the question, “if grouping is about seeing the big picture of the scene, how are certain small visual outlier popout so clearly, even though there is nothing common between them?” The key insight is that pair-wise repulsions, derived from feature dissimilarity, play an important role in making a set of dissimilar visual elements look salient. By analyzing the patterns of pair-wise pixel repulsion, in addition to pair-wise pixel attraction, we not only can provide a computational mechanism for popout, but also derive a global energy function for analyzing the necessary conditions for visual popout.
"Grouping with Bias"
Stella Yu and Jianbo Shi
Conference on Neural Information Processing Systems (NIPS'01), Vancouver, BC, December 3-5, 2001 paper
In this paper, our goal is to narrow the gap between the discriminative and generative grouping approaches. We are particularly interested in how partial grouping information, which might come from a generative color/texture models, user hand inputs, or attention, can be included in the discriminative grouping approach of Ncut. A naïve way to achieve this would be to 1) over segment the image first, and 2) regroup the segments with generative grouping information. We show that this can be done in one step, by encoding the partial grouping information as a linear subspace constraint on the pixel-group indicating variables. Together this leads to an eigen-decomposition problem with a linear constraint, which also has an efficient computational solution. We are currently working on automatically generating these “biases” using familiar shape configuration.
"Segmentation with Directed Relationships"
Stella Yu and Jianbo Shi
Third International Workshop on Energy Minimization
Methods in Computer Vision and Pattern Recognition(EMMCVPR'01 ), INRIASophia-Antipolis,
We are motivated by the figure-ground segmentation problem. This problem leads us to explore the use of negative graph weights (which has been mostly avoided in the previous graph cuts algorithms), and directed graph weights. With this type of general graph weights, we can specify local figure-group preferences, and using the properties of Ncut to find a global figure-group segmentation configuration. Computationally, this reduces to a complex valued eigen-value problem, which is interesting to us in itself.