Camillo J. Taylor, GRASP Lab, University of
Pennsylvania - [home]
Reconstruction of Linearly Parameterized Models from Single
Images
Abstract
This work deals with the problem of recovering the dimensions
of an object and its pose from a single image acquired with a
camera of unknown focal length. It is assumed that the object
in question can be modeled as a polyhedron where the coordinates
of the vertices can be expressed as a linear function of a dimension
vector. The reconstruction program takes as input a set of correspondences
between features in the model and features in the image. From
this information the program determines an appropriate projection
model for the camera (scaled orthographic or perspective), the
dimensions of the object, its pose relative to the camera and,
in the case of perspective projection, the focal length of the
camera. This paper describes how the reconstruction problem can
be framed as an optimization over a compact set with low dimension
- no more than four. This optimization problem can be solved efficiently
by coupling standard non-linear optimization techniques with a
multistart method which generates multiple starting points for
the optimizer by sampling the parameter space uniformly. The result
is an efficient, reliable solution system that does not require
initial estimates for any of the parameters being estimated.
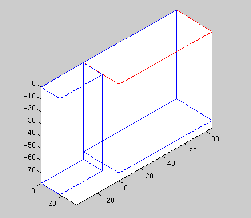
 Input Imagery
Input Imagery
|
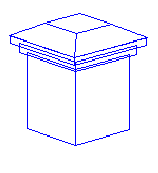 Recovered Model
Recovered Model
|
Related Publications
Useful Links
- David Jelinek maintains a slightly more detailed version
of this information on this
page




 Input Imagery
Input Imagery