Homework 3: Hail, Caesar!

0. Background

---

B. Background

Cryptography is the study of secure communications and secret codes. It helps you, say, send a secret message across enemy lines, knowing that even if the message is intercepted, it could not be read. People have been using ciphers (encrypted messages) for thousands of years, but only in the last century have computers come into the field. One of the oldest ways to hide a message is to use a substitution cipher. One classic example of a substitution cipher is the Caesar cipher, named after the first recorded (and most famous) user, Julius Caesar. If you'd like to learn more about the Caesar cipher, you can check out the wikipedia page to read about its history and usage.

C. Understanding the Problem

The Caesar cipher is a basic encryption technique where all letters in a message are shifted down the alphabet by a certain number. In order to encrypt or decrypt a message, you will need a secret key that should, in practice, be hard to find if you don’t already know it. In the Caesar cipher, the key is the number of places to shift each character. This number could be specified numerically (e.g., 4) or it could be specified as a character (e.g., 'E' -- which is 4 places over from 'A'). To make it simpler, we typically convert the entire message to uppercase, and may omit punctuation.

For instance, consider the message (and famous Julius Caesar quote): "CAESAR’S WIFE MUST BE ABOVE SUSPICION" and the key "E", which says to shift each letter to the right four places in the alphabet. For example, 'C' becomes 'G', 'A' becomes 'E', etc. Note the letter 'W' in "WIFE", when shifted four down, goes beyond 'Z'. This is handled by wrapping back to the front of the alphabet, and so 'W' becomes 'A'.

In total, the message becomes:

GEIWEV'W AMJI QYWX FI EFSZI WYWTMGMSR

D. Program Requirements and Interface

By the end of this assignment, you will have a Caesar program takes in command line arguments that will tell it whether to

1. encrypt a message using a particular key,
2. decrypt a message using a particular key, or
3. crack an encrypted message, giving us back the secret key.

The message will be stored in a file, which will be read by the program.

To encrypt the message stored in plaintext.txt with a key of 'G', you would call

 java Caesar encrypt plaintext.txt G

To decrypt the message stored in cipher.txt with a key of 'G', you would call

 java Caesar decrypt cipher.txt G

To crack the message stored in cipher.txt, you would call

 java Caesar crack cipher.txt english.txt

E. Getting Started

Begin by creating a main class file named Caesar.java. Be sure to put all of your code in this file. Also download the following files and store them in the same directory: english.txt, encrypted_message.txt, and readme_caesar.txt.

1. Representing Symbols

---

A. Understanding the Representation

Before we begin encrypting messages, we first need to decide how to represent a message in our program. The obvious choice would be to store them as a String. This would certainly work, but may not be the easiest approach.

Instead, we will represent the message as an array of integers, where each integer is a symbol in the message. All English letters will be represented by their place in the alphabet. For instance, "C" is the third letter in the alphabet, and so would be represented by a 2. Remember, computer science loves zero-indexing, so the first letter, "A", would be 0. The word "CONSUL" would be represented as [ 2, 14, 13, 18, 20, 11 ].

Recall that Java already encodes characters as integers using ASCII:

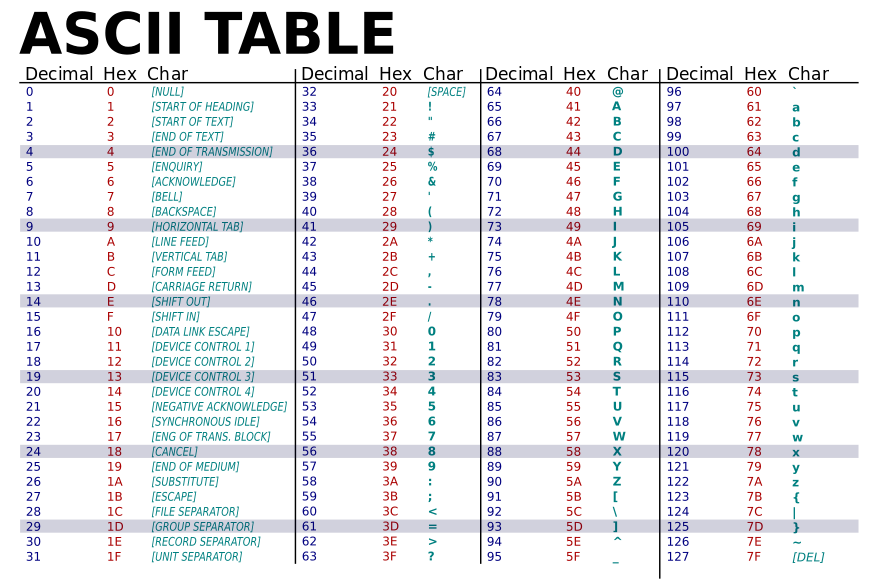
There is no need to memorize this, since we can easily recover the integer encoding via casting. For instance, take a look at this code snippet:

char letter = ‘A’;

// cast letter to an integer as encoded by ASCII
int asciiRepresentation = (int) letter;

// will print out 65
System.out.println(asciiRepresentation); 
        

We could certainly use ASCII to encode characters as integers in this program, but the math is a bit easier if we instead represent 'A' as 0 instead of 65. Fortunately, there is a very simple way of converting between the ASCII encoding and our symbol encoding. We can simply subtract or add the character 'A':

char letter = ‘C’;

// cast letter to an integer as encoded by our representation
int ourSymbolRepresentation = (int) letter - 'A';

// will print out 2
System.out.println(ourSymbolRepresentation); 
        

We can easily recover the original character simply by adding 'A' to it:

int ourSymbolRepresentation = 2;

// will become 'C'
char letter = (char) (ourSymbolRepresentation + 'A');
        

You should play around in the interactions pane so to fully understand how to make this switch, before moving on to the next section.

B. Program Structure Decomposition

Recall that functions allow us to intelligently decompose our program into a collection of logical units that we can develop and test independently. We can often identify these major units by considering the high level structure of our program and what we will need to do.

Recall that your Caesar program must take in command line arguments that will tell it whether to

1. encrypt a message using a particular key,
2. decrypt a message using a particular key, or
3. crack an encrypted message, giving us back the secret key.

The message will be stored in a file, which will be read by the program.

Based solely on this description, we can see that we will need three high-level functions:

1. encrypt(),
2. decrypt(), and
3. crack().

The main() will then serve as the overall control for our program, reading the command line arguments, reading in the text from the file, and calling the appropriate functions.

We can also see that many of these functions will need to convert between text and the integer symbol encoding, and handle the shifting. In fact, these procedures are likely to be so common that we should make helper functions to handle them.

For example, our basic encryption/decryption process will need to:

1. take in text as a String and convert it into our symbol encoding
2. shift that encoding either right (to encrypt) or left (to decrypt)
3. convert that symbol encoding back into text for output

With this decomposition, our task will then be to write functions for each of these major units (which we can do and test independently), and then combine those functions together into a working program.

C. Converting To and From Symbol Arrays

We will first tackle the lowest-level functions to handle encoding/decoding of strings (items 1 and 3 in the last list above) by writing two functions: one to convert from a String to our symbol representation (an array of integers), and one to convert from our symbol representation (an array of integers) to a String:

/*
 * Description: converts a string to a symbol array, where each element of the array 
 *              is an integer encoding of the corresponding element of the string.
 * Input:  the message text to be converted
 * Output: integer encoding of the message
 */
public static int[] stringToSymbolArray(String str) { ... }

/*
 * Description: converts an array of symbols to a string, where each element of the 
 *              array is an integer encoding of the corresponding element of the string.
 * Input:  integer encoding of the message
 * Output: the message text
 */
public static String symbolArrayToString(int[] symbols) { ... }
        

stringToSymbolArray() should initialize an integer array of the correct length, iterate through each character in str to fill in the indices in the array with the corresponding symbol integer value. Recall that you can use str.charAt(i) to find the ith character in str and your knowledge of ASCII to make the conversion from char to the symbol integer.

Note: you should use the str.toUpperCase() before converting. This will simply make all alphabet characters become uppercase.

Test this first function by writing a bit of test code in your main() function to call stringToSymbolArray("CONSUL") and check that the function call returns the array [ 2, 14, 13, 18, 20, 11 ]. Try a few other test cases. Once you're convinced the function is working, move on to write symbolArrayToString().

symbolArrayToString() should take an integer array where each element is the symbol value for the corresponding letter. The structure of this function is similar to stringToSymbolArray(), except it reverses the process.

Again, write code in main() to test symbolArrayToString(). Since you know that stringToSymbolArray() is working, your test code can use this function to encode a simple string, and then use symbolArrayToString() to decode it. If it works correctly, you should get back the same simple string you encoded. Test your code until you're convinced both functions work.

D. Shifting Symbols

The next step is to write a function to handle the shifting. We can define it as:

 public static int shift(int symbol, int offset) 

If symbol is an english letter (between 0 and 25), then it should be shifted down the alphabet by offset amount (an integer between 0 and 25). Remember to wrap symbols that go off the alphabet (‘W’ shifted by ‘E’ should return 0 representing ‘A’)!

If symbol is not between 0 and 25, meaning it is some sort of whitespace or punctuation, then it should just be returned as is. (In our implementation, punctuation is not encoded and does not change during the encryption/decryption process.)

Hint: Modulo (%) will be helpful here!

Write an appropriate header comment for your shift() function.

E. Unshifting Symbols

It may also be helpful for us to handle the unshifting (i.e., left shifting) of characters. Write a function to unshift the characters:

 public static int unshift(int symbol, int offset) 

This should simply undo the shifts done by shift(). Try thinking about how you will do this and do some examples before writing any code! Also, try to think how you can very easily do this by building on code you've already written.

F. Other Functions

While writing your program, you may find it useful to define other helper functions for processes that you are doing repeatedly. Feel free to define whatever other functions you need to while writing your program.

2. The Caesar Cipher

---

Now that we've defined functions to handle the encoding/decoding and shifting, we can focus on the three high-level functions in our program decomposition:

1. encrypt(),
2. decrypt(), and
3. crack().

The main() will then serve as the overall control for our program, reading the command line arguments, reading the text from the file, and calling the appropriate functions.

We will start by defining encrypt()....

A. Encrypt

Using the functions you have already written, you should write the function:

 public static String encrypt(String message, int key) 

The basic operations carried out in the function should be to:

• convert the message to an array of symbols (which we represent as ints)
• for each alphabetic symbol in the array, shift it by the given key
• return a String version of the encrypted symbol array

Once this is done, you should be able to test encrypt() in main() and be able to encrypt "ET TU, BRUTE?" using 6 (letter G) as the key to get "KZ ZA, HXAZK?".

Be sure to write good header comments for the function, and test it thoroughly before proceeding to the next part.

B. Decrypt

Now that you can encrypt your message, you need to be sure you can decrypt it. Write the decrypt function:

 public static String decrypt(String cipher, int key) 

The structure of this function is very similar to encrypt(), but instead of using shift, you should be using unshift.

Once this is done, you should be able to use decrypt() in main() with "KZ ZA, HXAZK?" and 6 (letter G) as the key to obtain "ET TU, BRUTE?".

You should add some code in main() to test it. At this point, if you run a string through encrypt() and then decrypt(), the output should be the same as the input string.

Try putting this or something similar in your main():

String message = "I AM CONSTANT AS THE NORTHERN STAR";
String cipher = encrypt(message, /* some key */);
String decrypted = decrypt(cipher, /* same key */);
System.out.println(decrypted); // should be the original message (in upper case)
        

C. Reading From a File

Once you are confident that encrypt() and decrypt() are working, you should comment out anything you’ve written in your main(). In order to obtain the message you will be encrypting you will need to read in data from a file.

Look back at your NBody.java from last week and make use of In inStream to do this. The function that will be most helpful is inStream.readAll() which returns the entire text of the file as a String.

Write code in main to handle the command line arguments, load the specified text file, call the appropriate function to encrypt/decrypt the message, and output the result.

Before you move on to the next part, you should be able to run

 java Caesar encrypt filename.txt G 

to encrypt the message in filename.txt using G (symbol value 6) as the key, and

 java Caesar decrypt filename.txt G 

to decrypt the message in filename.txt using G (symbol value 6) as the key.

If you’d like a refresher on command-line arguments or reading from a file, you can look at NBody.

3. Cracking the Cipher

---

A. Understanding the Process

The first recorded instance of a systematic breaking of the Caesar cipher came from Al-Kindi in Mesopotamia in the 9th Century: almost 1000 years after Caesar’s death!

In order to break the cipher, you will be employing letter frequency analysis. This simply means taking a text or String and seeing how often each letter appears. English text will have lots of "E"s and "A"s, while an encrypted cipher may have an unusual number of "X"s or "B"s.

B. Letter Frequency Analysis

Before you can analyze the ciphertext to crack it, you will need the frequencies of letters in english. We have given these frequencies for each letter in a file english.txt. The first line will have the frequency of the letter ‘A’, the second ‘B’, and so on. You should take a look at the file, and note that it has 26 lines.

Write a function called getDictionaryFrequencies() that takes as input the name of the file and returns a double array with the frequencies. The 0th element in the array should be the frequency of ‘A’, the 1st should be the frequency of ‘B’, and so on.

Note: from here on, it will be your responsibility to write the function headers and good header comments!

Once you have the frequencies of characters in English it is time to obtain the frequencies in the ciphertext. In order to do this write a helper function titled findFrequencies(). The input will be the symbol array (int[]) and it should return a double array where the 0th element in the array is the frequency of ‘A’ in the ciphertext, and so on.

To find the frequency of each letter, first find the number of times each letter appears in the ciphertext. Then, divide all by the total number of letters in the ciphertext. Ignore any non-letter symbol.

Write code to test your functions. (Hint: Make a simple string with a known letter frequency, encode it, and make sure your findFrequencies() gives you back the appropriate frequency counts.)

C. Scoring the Frequency

The next step in cracking the cipher will be scoring the frequencies you found in the last step. This is done by finding the absolute value of the difference between each letter in the ciphertext frequencies and its corresponding letter in the english frequencies.

For example, given an array for frequencies of A, B, and C in a message as [ 0.2, 0.1, 0.0 ] and the english language frequencies is [ 0.1, 0.1, 0.05 ]. The total score of the messsage's frequencies would be:

 Math.abs(0.2 - 0.1) + Math.abs(0.1 - 0.1) + Math.abs(0.0 - 0.05) = 0.15 

This score essentially tells us how well the letter frequency in the message matches what we would expect if the message were in English. The lower the score, the better. We can use this later to crack the Caesar cipher by trying different keys and picking the one that gives us the lowest score!

Write the function scoreFrequencies() that takes in two frequencies arrays, freqs and englishFreqs, and returns the difference between each value pair in the arrays, as described above.

D. Cracking Caesar

Now for the fun part. The written decryption and encryption code allows us to be able to hide and decipher cool messages but what if we don’t know the key? In order to crack a cipher with an unknown key we can guess the key via brute force until we find the correct one.

One method to do this is to try to decrypt the cipher message with all possible keys (‘A’ through ‘Z’). At each decryption find the frequencies of the letters in our newly decrypted message and use this to determine the frequency score (using scoreFrequencies()). You want to find which key will give us a message that looks most similar to English, so its frequency score should be the lowest among all keys.

Finding the minimum score key will be a similar process as finding the minimum value in an array, so looking back at that example from lecture and recitation may be helpful.

Once you’ve tried decrypting with all possible keys, return the message found using the key with the lowest score. This should be the original message!

You should be writting a function called crack() to perform these steps. We'd like you to think about what the inputs to this function should be, what it should return, and whether you'd like any other functions to help you out. There are several correct ways to do this, so really think about the benefits and drawbacks to your design!

E. Final Touches

Once you have written crack(), you should add code to your main so that you can run Caesar.java using:

 java Caesar crack cipher.txt english.txt

This command will crack the cipher in cipher.txt, using the letter frequencies stored in english.txt, which your program must also load. It should print out the cracked message.

Once you have this working, and tested crack(), you have a program that can encrypt a message, decrypt it with the key, and break encryption. You've just cracked Caesar!

Try out your program by downloading encrypted_message.txt, an encrypted message we've provided for you, and crack it without the key. Put the answer to this in your readme_caesar.txt.

4. Extra Credit

---

RSA XLEX CSY LEZI GSQTPIXIH XLI GEIWEV GMTLIV (ERH GER VIEH XLMW IBXVE GVIHMX HIWGVMTXMSR!), XVC E FMKKIV GLEPPIRKI!

EW IBXVE GVIHMX, MQTPIQIRX E TVSKVEQ XS IRGVCTX ERH HIGVCTX QIWWEKIW YWMRK XLI ZMKIRIVI GMTLIV.  XLI ZMKIRIVI GMTLIV YWIW E WIVMIW SJ HMJJIVIRX GEIWEV GMTLIVW XS IRGVCTX XIBX, FEWIH SR XLI PIXXIVW SJ E OICASVH.  PSSO MX YT SR AMOMTIHME JSV HIXEMPW EW XS LSA XLI ZMKIRIVI GMTLIV ASVOW. (WSVVC, FYX AI GSYPHR'X HMVIGXPC MRGPYHI XLI PMRO, WMRGI XLMW IBXVE GVIHMX XIBX MW IRGVCTXIH!)

AVMXI E TVSKVEQ XS IRGVCTX ERH HIGVCTX QIWWEKIW YWMRK XLI ZMKIRIVI GMTLIV.  CSYV TVSKVEQ WLSYPH FI REQIH "ZMKIRIVI" (FYX MR GEQIP GEWI, RSX EPP YTTIVGEWI) ERH MX WLSYPH JSPPSA E GSQQERH PMRI MRXIVJEGI WMQMPEV XS XLI GEIWEV TVSKVEQ.  XLI SRI HMJJIVIRGI MW XLEX MRWXIEH SJ XEOMRK MR E PIXXIV EW XLI OIC, MX AMPP EGGITX ER IRXMVI ASVH.  JSV ER IBXVE GLEPPIRKI, XVC GVEGOMRK XLI ZMKIRIVI GMTLIV.

KSSH PYGO!
                

5. Readme and Submission

---

A. README

Complete readme_caesar.txt in the same way you have done for previous assignments.

B. Submission

Submit Caesar.java and readme_caesar.txt on the course website. If you have completed extra credit please mention this in the readme, and submit it compressed as extra.zip.

Before submission remove any print statements that were used for debugging or testing your functions.

Be sure that every method has an appropriate header comment, and that your code is well-documented.