Nested Words

aka Visibly Pushdown Languages

What are nested words?

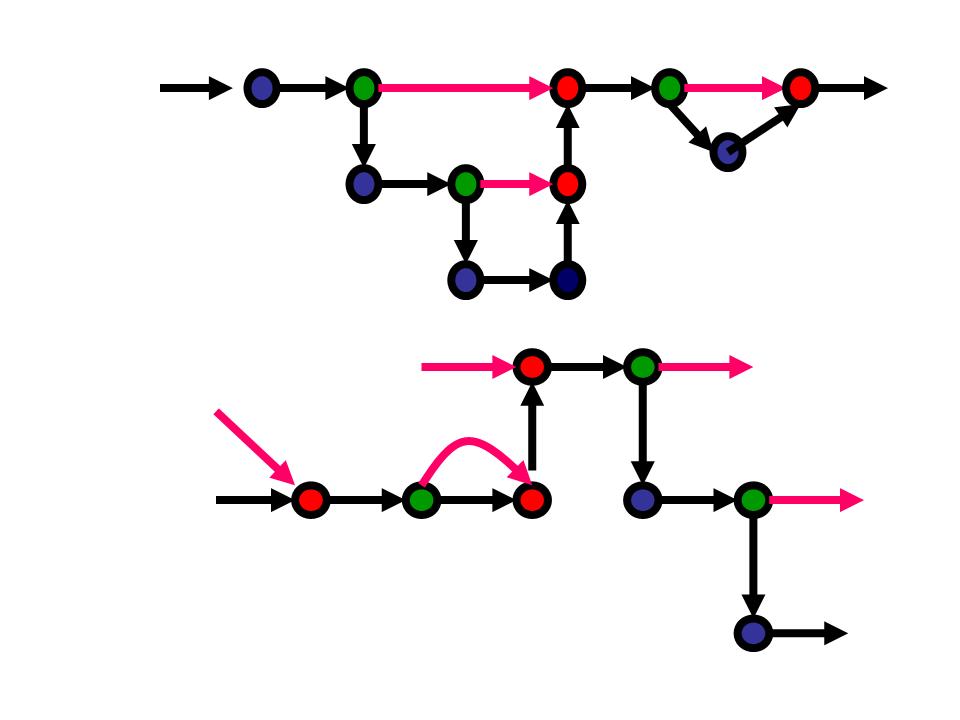Nested words is a model for representation of data with both a linear ordering and a hierarchically nested matching of items. Examples of data with such dual linear-hierarchical structure include executions of structured programs, annotated linguistic data, and HTML/XML documents. A nested word consists of a sequence of linearly ordered positions, augmented with nesting edges connecting calls to returns (or open-tags to close-tags). The edges do not cross creating a properly nested hierarchical structure, and we allow some of the edges to be pending. This nesting structure can be uniquely represented by a sequence specifying the types of positions (calls, returns, and internals). Nested words generalize both words and ordered trees, and allow both word and tree operations.

Nested word automata---finite-state acceptors for nested words, define the class of regular languages of nested words. This class has all the appealing theoretical properties that the classical regular word languages enjoys: deterministic nested word automata are as expressive as their nondeterministic counterparts; the class is closed under union, intersection, complementation, concatenation, Kleene-*, prefixes, and language homomorphisms; membership, emptiness, language inclusion, and language equivalence are all decidable; and definability in monadic second order logic corresponds exactly to finite-state recognizability. These results generalize to infinite nested words also.

How do they relate to context-free languages of words?

Given a language L of nested words over an alphabet, the linear encoding of nested words gives a language L' over the tagged alphabet consisting of symbols tagged with the type of the position. If L is regular language of nested words, then L' is context-free. In fact, the pushdown automaton accepting L' has a special structure: while reading a call, the automaton must push one symbol, while reading a return symbol, it must pop one symbol (if the stack is non-empty), and while reading an internal symbol, it can only update its control state. We call such automata visibly pushdown automata and the class of word languages they accept visibly pushdown languages (VPL). Since our automata can be determinized, VPLs correspond to a subclass of deterministic context-free languages (DCFL). VPLs generalize of paranthesis languages, bracketed languages, and balanced languages, and they have better closure properties than CFLs, DCFLs, or paranthesis languages.

We argue that for algorithmic verification of structured programs, instead of viewing the program as a context-free language over words, one should view it as a regular language of nested words (or equivalently, a visibly pushdown language), and this would allow model checking of many properties (such as stack inspection, pre-post conditions) that are not expressible in existing specification logics.

In general, pushdown automata serve two distinct purposes: discovering the hierarchical matching, and processing/querying the matching. In applications where only the second purpose is relevant (as in program analysis), one can replace pushdown automata with NWAs with many benefits.

How do they relate to ordered trees?

Data with dual linear-hierarchical structure is traditionally modeled using binary, and more generally, using ordered unranked, trees, and queried using tree automata. In ordered trees, nodes with the same parent are linearly ordered, and the classical tree traversals such as infix (or depth-first left-to-right) can be used to define an implicit ordering of all nodes. It turns out that, hedges, where a hedge is a sequence of ordered trees, are a special class of nested words, namely, the ones corresponding to Dyck words, and regular hedge languages correspond to balanced languages.

For document processing, nested words do have many advantages over ordered trees. Tree-based representation implicitly assumes that the input linear data can be parsed into a tree, and thus, one cannot represent and process data that may not parse correctly. Word operations such as prefixes, suffixes, and concatenation, while natural for document processing, do not have analogous tree operations. Second, tree automata can naturally express constraints on the sequence of labels along a hierarchical path, and also along the left-to-right siblings, but they have difficulty to capture constraints that refer to the global linear order. For example, the query that patterns p1,... pk appear in the document in that order compiles into a deterministic word automaton (and hence deterministic NWA) of linear size, but standard deterministic bottom-up tree automaton for this query must be of size exponential in k. NWAs can be viewed as a kind of tree automata such that both bottom-up tree automata and top-down tree automata are special cases. These results imply that a query can be more succinctly encoded in the nested words view with complexity benefits A nested word automaton reads the word from left to right, processing the nesting edges as and when they arrive. This matches with the SAX API for XML, and thus has a natural use in streaming algorithms.

References

The model of nested words went through a couple of iterations: See Visibly pushdown languages; Alur and Madhusudan; STOC 2004; and Adding nesting structure to words; Alur and Madhusudan; DLT 2006. We recommend reading this unified full version (Journal of the ACM, 2009). The invited talk at CSR 2007 is also a good starting point.

The purpose of this page is to keep track of the extensive follow-up research on this topic. Email me with comments and/or suggested additions.

Tools

Additional Decision Problems for VPAs/NWAs

Congruences and Minimization

Temporal and Fixpoint Logics; Expressiveness

Specifications for Program Analysis

XML Processing and Tree Automata

Transducers

Nested Trees

Words with Multiple Nestings

New Results Using Visibility of Calls/Returns

A Challenging Open Problem (Now Solved!)

Consider the following decision problem: given two regular languages L1 and L2 of nested words, does there exist a regular language R of words over the tagged alphabet such that Intersection(R,L1) equals L2? This is not known to be decidable, even for the special case that L1 is the set of all well-matched words. The motivation is the following: in general, to check whether the input belongs to L2, the processing machine needs a stack. But suppose we already have some additional knowledge about the input, that it belongs to the set L1 (for example, we may know that the input is well-matched), can this knowledge be used to construct a DFA A such that for inputs in L1, A is able to decide membership in L2. This problem is inspired by the paper "Validating streaming XML documents" by Segoufin and Vianu, PODS 2002, which also presents a partial solution.

Recently, Eryk Kopczynski has proved undecidability of this problem: see Invisible pushdown languages, LICS 2016.

View this page in Romanian courtesy of azoft
Slovakian translation created by Sciologness Team
Czech translation created by Kate Bondareva
Russian translation created by Boostpack
Greek translation courtesy of Dimitris Galatas
Polish translation by Weronika Pawlak
Estonian translation by Karolin Lohmus
Maintained by Rajeev Alur